α-koefficienten är det mest använda förfarandet för att uppskatta tillförlitlighet i tillämpad forskning. Som framgår av Sijtsma (2009) är dess popularitet sådan att Cronbach (1951) har citerats som en referens oftare än artikeln om upptäckten av DNA double helix., Ändå är dess begränsningar välkända (Lord and Novick, 1968; Cortina, 1993; Yang and Green, 2011), några av de viktigaste är antagandena om okorrelaterade fel, tau-ekvivalens och normalitet.
antagandet av okorrelerade fel (felpoängen för ett par objekt är okorrelerat) är en hypotes om klassisk Testteori (Lord och Novick, 1968), vars överträdelse kan innebära närvaron av komplexa flerdimensionella strukturer som kräver uppskattningsförfaranden som tar hänsyn till denna komplexitet (t. ex. Tarkkonen och Vehkalahti, 2005; Green and Yang, 2015)., Det är viktigt att utrota den felaktiga tron Att α-koefficienten är en bra indikator på unidimensionalitet eftersom dess värde skulle vara högre om skalan var ensidig. Faktum är att det exakta motsatsen är fallet, vilket visades av Sijtsma (2009), och dess tillämpning under sådana förhållanden kan leda till att tillförlitligheten är kraftigt överskattad (Raykov, 2001). Därför är det nödvändigt att kontrollera att uppgifterna passar endimensionella modeller innan man beräknar α.
antagandet om tau-ekvivalens (dvs.,, samma sanna poäng för alla testposter, eller lika faktorbelastningar av alla objekt i en faktoriell modell) är ett krav på att α ska motsvara tillförlitlighetskoefficienten (Cronbach, 1951). Om antagandet om tau-ekvivalens bryts kommer det verkliga tillförlitlighetsvärdet att underskattas (Raykov, 1997; Graham, 2006) med ett belopp som kan variera mellan 0,6 och 11,1% beroende på överträdelsens allvar (grön och Yang, 2009a). Att arbeta med data som överensstämmer med detta antagande är i allmänhet inte genomförbart i praktiken (Teo och Fan, 2013); Den kongeneriska modellen (dvs.,, olika faktorbelastningar) är ju mer realistiska.
kravet på multivariant normalitet är mindre känt och påverkar både den puntuella tillförlitlighetsuppskattningen och möjligheten att fastställa konfidensintervall (Dunn et al., 2014). Sheng och Sheng (2012) observerade nyligen att när fördelningarna är sneda och / eller leptokurtiska produceras en negativ bias när koefficienten α beräknas.liknande resultat presenterades av Green and Yang (2009b) i en analys av effekterna av icke-normala fördelningar vid uppskattning av tillförlitlighet., Studie av skevhetsproblem är viktigare när vi ser att forskare i praktiken vanligtvis arbetar med sneda skalor (Micceri, 1989; Norton et al. 2013; för Ho och Yu, 2014). Till exempel uppskattade Micceri (1989) att cirka 2/3 av förmågan och över 4/5 av psykometriska åtgärder uppvisade minst måttlig asymmetri (dvs skevhet runt 1). Trots detta har effekten av skevhet på tillförlitlighetsuppskattning inte studerats tillräckligt.,
med Tanke på den rikliga litteratur på de begränsningar och fördomar av α-koefficient (Revelle och Zinbarg, 2009; Sijtsma, 2009, 2012; Cho och Kim, 2015; Sijtsma och van der Arken, 2015), uppstår frågan varför forskare fortsätta att använda α när alternativa koefficienter som finns övervinna dessa begränsningar. Det är möjligt att överskottet av förfaranden för att uppskatta tillförlitlighet som utvecklats under det senaste århundradet har svängt debatten. Detta skulle ha förstärkts ytterligare av enkelheten i beräkningen av denna koefficient och dess tillgänglighet i kommersiella programvaror.,
svårigheten att uppskatta PXX ’tillförlitlighet koefficient finns i sin definition PXX’ =σt2 σx2, vilket inkluderar den verkliga poängen i varians täljare när detta är av naturen unobservable. Α-koefficienten försöker approximera denna icke observerbara varians från kovariansen mellan objekten eller komponenterna. Cronbach (1951) visade att i avsaknad av tau-ekvivalens var α-koefficienten (eller Guttman”s lambda 3, vilket motsvarar α) En bra lägre bunden approximation., Således, när de antaganden som kränks problemet leder till att hitta den bästa möjliga nedre gräns, ja detta namn ges Största Nedre gräns metod (GLB) som är den bästa möjliga tillnärmning från en teoretisk vinkel (Jackson och Agunwamba, 1977; Woodhouse och Jackson, 1977; Shapiro och tio Berge, 2000; Sočan, 2000; ten Berge och Sočan, 2004; Sijtsma, 2009). Revelle och Zinbarg (2009) anser dock att ω ger en bättre lägre gräns än GLB., Det finns därför en olöst debatt om vilken av dessa två metoder som ger den bästa lägre gränsen. dessutom har frågan om icke-normalitet inte undersökts uttömmande, som det nuvarande arbetet diskuterar.
ω koefficienter
McDonald (1999) föreslog WT-koefficienten för att uppskatta tillförlitligheten från en faktoriell analysram, som formellt kan uttryckas som:
där λj är lastningen av punkt j, λj2 är gemenskapligheten av punkt j och motsvarar det unika., WT-koefficienten, genom att inkludera lambdas i dess formler, är lämplig både när tau-ekvivalens (dvs lika faktorbelastningar för alla testämnen) existerar (wt sammanfaller matematiskt med α), Och när objekt med olika diskrimineringar är närvarande i konstruktionens representation (dvs olika faktorbelastningar av objekten: kongeneriska mätningar). Följaktligen korrigerar WT underskattningens bias när antagandet om tau-ekvivalens bryts (Dunn et al., 2014) och olika studier visar att det är ett av de bästa alternativen för att uppskatta tillförlitlighet (Zinbarg et al.,, 2005, 2006; Revelle och Zinbarg, 2009), men hittills är dess funktion under förhållanden med skevhet okänd.
När samband mellan fel, eller om det är mer än en latent dimensionen i data, ska bidraget från varje dimension till den totala variansen som förklaras är uppskattade, att få den så kallade hierarkiska ω (wh) som gör det möjligt för oss att rätta till de värsta överskattning överskattning på α med flerdimensionella data (se Tarkkonen och Vehkalahti, 2005; Zinbarg et al., 2005; Revelle och Zinbarg, 2009)., Koefficienter wh och wt är likvärdiga i unidimensional data, så vi kommer att hänvisa till denna koefficient helt enkelt som ω.
Greatest Lower Bound (GLB)
Sijtsma (2009) visar i en serie studier att en av de mest kraftfulla uppskattningarna av tillförlitlighet är GLB—härledd av Woodhouse och Jackson (1977) från antagandena om klassisk Testteori (CX = Ct + Ce)—en inter-post covariance matris för observerade objektpoäng CX. Det bryts ner i två delar: summan av kovariansmatrisen mellan objektet för objektet true scores Ct; och Inter-item error covariance matrix Ce (ten Berge och Sočan, 2004)., Dess uttryck är:
där σx2 är testvariansen och tr(Ce) refererar till spåret av Inter-objektfelkovariansmatrisen som det har visat sig vara så svårt att uppskatta. En lösning har varit att använda faktoriella förfaranden som Minimum Rank Factor Analysis (ett förfarande som kallas glb.fa). Mer nyligen GLB algebraiska (GLBa) förfarandet har utvecklats från en algoritm som utarbetats av Andreas Moltner (Moltner och Revelle, 2015)., Enligt Revelle (2015a) antar detta förfarande den form som är mest trogen mot den ursprungliga definitionen av Jackson och Agunwamba (1977), och det har den extra fördelen att införa en vektor för att väga föremålen av betydelse (Al-Homidan, 2008).
trots dess teoretiska styrkor har GLB använts mycket lite, även om vissa nyligen genomförda empiriska studier har visat att denna koefficient ger bättre resultat än α (Lila et al., 2014) och α och ω (Wilcox et al., 2014)., Men i små prover, enligt antagandet om normalitet, tenderar det att överskatta det sanna tillförlitlighetsvärdet (Shapiro och ten Berge, 2000). men dess funktion under icke-normala förhållanden är fortfarande okänd, speciellt när fördelningarna av objekten är asymmetriska.
Med tanke på de koefficienter som definieras ovan, och fördomar och begränsningar av varje, är syftet med detta arbete att utvärdera robustheten hos dessa koefficienter i närvaro av asymmetriska objekt, med tanke på antagandet om tau-ekvivalens och provstorleken.,
metoder
datagenerering
data genererades med hjälp av R (R Development Core Team, 2013) och RStudio (Racine, 2012) programvara, efter faktoriell modell:
där Xij är det simulerade svaret av ämne i i punkt j, λjk är laddningen av punkt J i faktor K (som genererades av Unifaktoriell modell); FK är den latenta faktorn som genereras av en standardiserad normalfördelning (medelvärde 0 och varians 1), och ej är det slumpmässiga mätfelet för varje objekt som också följer en standardiserad normalfördelning.,
skeva objekt: Standard normal Xij omvandlades för att generera icke-normala distributioner med hjälp av det förfarande som föreslagits av Headrick (2002) med tillämpning av femte ordningens polynomtransformer:
simulerade förhållanden
för att bedöma prestandan hos tillförlitlighetskoefficienterna (α, ω, ω, GLB och GLBA) vi arbetade med tre provstorlekar (250, 500, 1000), två teststorlekar: korta (6 objekt) och långa (12 objekt), två villkor för tau-ekvivalens (en med tau-ekvivalens och en utan, dvs,, kongenerisk) och den gradvisa införlivandet av asymmetriska poster (från alla poster är normala till alla poster är asymmetriska). I det korta testet ställdes tillförlitligheten vid 0,731, vilket i närvaro av tau-ekvivalens uppnås med sex punkter med faktorbelastningar = 0,558; medan den kongeneriska modellen erhålls genom att ställa in faktorbelastningar vid värden av 0.3, 0.4, 0.5, 0.6, 0.7, och 0, 8 (SE tillägg I). I det långa testet av 12 objekt sattes tillförlitligheten till 0.,845 med samma värden som i det korta testet för både tau-ekvivalens och den kongeneriska modellen (i detta fall fanns det två poster för varje värde av lambda). På detta sätt simulerades 120 förhållanden med 1000 repliker i varje enskilt fall.
Analys av Data
De huvudsakliga analyserna genomfördes med hjälp av Psych (Revelle, 2015b) och GPArotation (Bernaards och Jennrich, 2015) paket, som gör att α och ω uppskattas. Två datoriserade metoder användes för att uppskatta GLB: glb.fa (Revelle, 2015a) och glb.,algebraic (Moltner och Revelle, 2015), den senare arbetade av författare som Hunt och Bentler (2015).
för att utvärdera noggrannheten hos de olika estimatorerna i att återställa tillförlitligheten beräknade vi Root Mean Square of Error (RMSE) och bias. Den första är medelvärdet av skillnaderna mellan den uppskattade och den simulerade tillförlitligheten och formaliseras som:
där ρ^ är den beräknade tillförlitligheten för varje koefficient, ρ den simulerade tillförlitligheten och Nr antalet repliker., Procentuell bias förstås som skillnaden mellan medelvärdet av den uppskattade tillförlitligheten och den simulerade tillförlitligheten och definieras som:
i båda indexen, desto större värde desto större är uppskattarens felaktighet, men till skillnad från RMSE kan bias vara positiv eller negativ.i detta fall skulle ytterligare information erhållas om huruvida koefficienten underskattar eller överskattar den simulerade tillförlitlighetsparametern., Efter rekommendation av Hoogland och Boomsma (1998) värden av RMSE < 0,05 och % bias < 5% ansågs godtagbara.
resultat
huvudresultaten kan ses i Tabell 1 (6 poster) och Tabell 2 (12 poster). Dessa visar RMSE och % bias av koefficienterna i tau-ekvivalens och kongeneriska förhållanden, och hur provfördelningens skevhet ökar med gradvis införlivande av asymmetriska föremål.
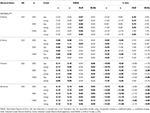
tabell 1., RMSE och Bias med tau-ekvivalens och kongeneriskt tillstånd för 6 objekt, tre provstorlekar och antalet sneda föremål.
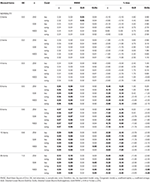
tabell 2. RMSE och Bias med tau-ekvivalens och kongeneriskt tillstånd för 12 objekt, tre provstorlekar och antalet sneda föremål.
endast under förhållanden med tau-ekvivalens och normalitet (skevhet< 0,2) är det observerat att α-koefficienten uppskattar den simulerade tillförlitligheten korrekt, som ω., I det kongeneriska tillståndet korrigerar ω underskattningen av α. Både GLB och GLBa uppvisar en positiv bias under normalitet, men GLBa visar ungefär ½ mindre % bias än GLB (se Tabell 1). Om vi betraktar provstorlek observerar vi att när teststorleken ökar minskar den positiva biasen av GLB och GLBa, men försvinner aldrig.
i asymmetriska förhållanden ser vi i Tabell 1 att både α Och ω uppvisar en oacceptabel prestanda med ökande RMSE och underskattningar som kan nå bias > 13% För α-koefficienten (mellan 1 och 2% lägre för ω)., GLB-och GLBa-koefficienterna ger en lägre RMSE när testspettheten eller antalet asymmetriska objekt ökar (se tabellerna 1, 2). GLB-koefficienten ger bättre uppskattningar när testspettvärdet för testet är runt 0.30; GLBa är mycket likartat och presenterar bättre uppskattningar än ω med ett testspettvärde runt 0.20 eller 0.30. Men när skevhetsvärdet ökar till 0,50 eller 0,60, ger GLB bättre prestanda än GLBa. Teststorleken (6 eller 12 ítems) har en mycket viktigare effekt än provstorleken på uppskattningarnas noggrannhet.,
diskussion
i denna studie manipulerades fyra faktorer: tau-ekvivalens eller kongenerisk modell, provstorlek (250, 500 och 1000), antalet testposter (6 och 12) och antalet asymmetriska föremål (från 0 asymmetriska föremål till alla objekt som är asymmetriska) för att utvärdera robusthet till närvaron av asymmetriska data i de fyra analyserade tillförlitlighetskoefficienterna. Dessa resultat diskuteras nedan.,
vid förhållanden med tau-ekvivalens konvergerar α-Och ω-koefficienterna, men i avsaknad av tau-ekvivalens (congeneric) presenterar ω alltid bättre uppskattningar och mindre RMSE och % bias än α. I detta mer realistiska tillstånd därför (grön och Yang, 2009a; Yang och grön, 2011), α blir en negativt partisk tillförlitlighet estimator (Graham, 2006; Sijtsma, 2009; Cho och Kim, 2015) och ω är alltid att föredra framför α (Dunn et al., 2014). Vid icke-överträdelse av antagandet om normalitet är ω den bästa estimatorn för alla utvärderade koefficienter (Revelle och Zinbarg, 2009).,
När vi vänder oss till provstorlek observerar vi att denna faktor har en liten effekt under normalitet eller en liten avvikelse från normalitet: RMSE och bias minskar när provstorleken ökar. Ändå kan det sägas att för dessa två koefficienter, med provstorlek på 250 och normalitet får vi relativt exakta uppskattningar (Tang och Cui, 2012; Javali et al., 2011)., För GLB-och GLBa-koefficienterna, eftersom provstorleken ökar RMSE och bias tenderar att minska; men de upprätthåller en positiv bias för normalitetsförhållandet även med stora provstorlekar på 1000 (Shapiro och ten Berge, 2000; ten Berge och Sočan, 2004; Sijtsma, 2009).
för teststorleken observerar vi generellt en högre RMSE och bias med 6 objekt än med 12, vilket tyder på att ju högre antal objekt desto lägre RMSE och bias av estimatorerna (Cortina, 1993). I allmänhet upprätthålls trenden för både 6 och 12 poster.,
När vi tittar på effekten av att gradvis införliva asymmetriska föremål i datauppsättningen, observerar vi att α-koefficienten är mycket känslig för asymmetriska föremål; dessa resultat liknar de som hittades av Sheng och Sheng (2012) och Green and Yang (2009b). Koefficient ω presenterar liknande RMSE-och biasvärden till α, men något bättre, även med tau-ekvivalens. GLB och GLBa finns att presentera bättre uppskattningar när testspett avgår från värden nära 0.
Med tanke på att det i praktiken är vanligt att hitta asymmetriska data (Micceri, 1989; Norton et al., 2013; för Ho och Yu, 2014), Sijtsma”s förslag (2009) med hjälp av GLB som en tillförlitlighet estimator verkar väl grundad. Andra författare, som Revelle och Zinbarg (2009) och Green and Yang (2009a), rekommenderar användningen av ω, Men denna koefficient gav bara bra resultat i normalitetsförhållandet eller med låg andel skevhetsartiklar. Under alla omständigheter presenterade dessa koefficienter större teoretiska och empiriska fördelar än α. Ändå rekommenderar vi forskare att studera inte bara punktliga uppskattningar utan också att använda intervalluppskattning (Dunn et al., 2014).,
dessa resultat är begränsade till de simulerade förhållandena och det antas att det inte finns någon korrelation mellan fel. Detta skulle göra det nödvändigt att genomföra ytterligare forskning för att utvärdera hur de olika tillförlitlighetskoefficienterna fungerar med mer komplexa flerdimensionella strukturer (Reise, 2012; Green and Yang, 2015) och i närvaro av ordinära och/eller kategoriska data där bristande överensstämmelse med antagandet om normalitet är normen.
slutsats
när de totala testpoängen normalt fördelas (dvs.,, alla objekt distribueras normalt) ω bör vara det första valet, följt av α, eftersom de undviker de överskattningsproblem som GLB presenterar. Men när det finns en låg eller måttlig test skewness GLBa bör användas. GLB rekommenderas när andelen asymmetriska objekt är hög, eftersom det under dessa förhållanden inte är lämpligt att använda både α Och ω Som tillförlitlighetsuppskattare, oavsett provstorlek.
Författarbidrag
utveckling av idén om forskning och teoretisk ram (IT, JA). Konstruktion av den metodologiska ramen (IT, JA)., Utveckling av R-språksyntaxen (IT, JA). Dataanalys och tolkning av data (IT, JA). Diskussion av resultaten mot bakgrund av aktuell teoretisk bakgrund (Ja, IT). Förberedelse och skrivning av artikeln (Ja, IT). I allmänhet har båda författarna bidragit lika till utvecklingen av detta arbete.,
finansiering
den första författaren avslöjade mottagandet av följande ekonomiska stöd för forskning, författarskap och/eller publicering av denna artikel: Det fick ekonomiskt stöd från den chilenska nationella kommissionen för vetenskaplig och teknisk forskning (CONICYT) ”Becas Chile” doktorandprogram (bidrag nr: 72140548).
intressekonflikt uttalande
författarna förklarar att forskningen genomfördes i avsaknad av kommersiella eller finansiella relationer som kan tolkas som en potentiell intressekonflikt.
Cronbach, L. (1951)., Koefficient alfa och testens interna struktur. Psykometrika 16, 297-334. doi: 10.1007/BF02310555
CrossRef Full Text | Google Scholar
McDonald’, R. (1999). Testteori: en enhetlig behandling. Lawrence Erlbaum Associates.
Google Scholar
r Development Core Team (2013). R: ett språk och en miljö för statistisk databehandling. Wien: R Grund för Statistiska Beräkningar.
Raykov, T. (1997)., Scale reliability, cronbach”s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package ”psych.,”Tillgänglig online på:http://org/r/psych-manual.pdf
Shapiro, A. och ten Berge, J. M. F. (2000). Den asymptotiska bias av minsta spårfaktoranalys, med applikationer till den största lägre bunden till tillförlitlighet. Psykometrika 65, 413-425. doi: 10.1007/BF02296154
CrossRef Full Text | Google Scholar
ten Berge, J. M. F., och Sočan, G. (2004). Den största lägre bunden till tillförlitligheten hos ett test och hypotesen om unidimensionalitet. Psykometrika 69, 613-625. doi: 10.,1007 / bf02289858
CrossRef Full Text | Google Scholar
Woodhouse, B., Och Jackson, P. H. (1977). Lägre gränser för tillförlitligheten av den totala poängen på ett test som består av icke-homogena objekt: II: ett sökförfarande för att lokalisera den största nedre gränsen. Psykometrika 42, 579-591. doi: 10.1007/BF02295980
CrossRef Full Text/Google Scholar
bilaga I
r syntax för att uppskatta tillförlitlighetskoefficienter från Pearsons korrelationsmatriser., Korrelationsvärdena utanför diagonalen beräknas genom att multiplicera faktorbelastningen av posterna: (1) tau-ekvivalent modell de är alla lika med 0.3114 (λiλj = 0.558 × 0.558 = 0.3114) och (2) kongenerisk modell de varierar som en funktion av den olika faktorbelastningen (t.ex. matriselementet a1, 2 = λ1λ2 = 0.3 × 0.4 = 0.12). I båda exemplen är den sanna tillförlitligheten 0,731.
> omega(Cr,1)$alpha # standardiserad Cronbach”s α
0.731
> omega(Cr,1)$omega.tot # koefficient ω totalt
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach”s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731