modellen Cox Proportional Hazards

jag skrev tidigare om hur man beräknar Kaplan–Meier-kurvan för överlevnadsdata. Som en icke-parametrisk estimator gör det ett bra jobb att ge en snabb titt på överlevnadskurvan för en datauppsättning. Men vad det inte låter dig göra är att modellera kovariates inverkan på överlevnad. I den här artikeln kommer vi att fokusera på Cox Proportional Hazards-modellen, en av de mest använda modellerna för överlevnadsdata.

Vi kommer att gå in på lite djup om hur man beräknar uppskattningarna., Detta är värdefullt eftersom vi kommer att se att uppskattningarna endast beror på beställning av misslyckanden och inte deras faktiska tider. Vi kommer också kortfattat att diskutera några knepiga frågor om kausal inferens som är speciella för överlevnadsanalys.

vi tänker vanligtvis på överlevnadsdata när det gäller överlevnadskurvor som den nedan.,

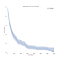
på x-axeln har vi tid på dagar. På Y-axeln har vi (en estimator för) procentandelen (Tekniskt, andel) av ämnen i befolkningen som ”överlever” till den tiden. Överleva kan vara figurativ eller bokstavlig., Det kan vara om människor lever i en viss ålder, om en maskin gör det en viss tid utan att bryta ner, eller det kan vara om någon förblir arbetslös en viss tid efter att ha förlorat sitt jobb.

avgörande är komplikationen i överlevnadsanalys att vissa ämnen inte har sin ”död” observerad. De kan fortfarande vara vid liv, en maskin kan fortfarande fungera, eller någon kan fortfarande vara arbetslös när uppgifterna samlas in., Sådana observationer kallas ”högercensurerade” och hantering av censur innebär att överlevnadsanalys kräver olika statistiska verktyg.

vi betecknar överlevnadsfunktionen som S, en funktion av tiden. Dess produktion är andelen ämnen som överlever vid tiden t. (återigen är det tekniskt en andel mellan 0 och 1, men jag kommer att använda de två orden omväxlande). För enkelhetens skull kommer vi att göra det tekniska antagandet att om vi väntar tillräckligt länge kommer alla ämnen att ”dö.”

Vi kommer att indexera ämnena med ett abonnemang som i eller j., Feltiderna för hela befolkningen kommer att anges med ett liknande subscript på tidsvariabeln t.

en annan subtilitet att överväga är om vi behandlar tid som diskret (vecka för vecka, säg) eller kontinuerlig. Filosofiskt sett mäter vi bara tid i diskreta steg (till närmaste sekund, säg)., Vanligtvis kommer våra data bara att berätta om någon dog under ett visst år eller om en maskin misslyckades på en viss dag. Jag kommer att gå fram och tillbaka mellan de diskreta och kontinuerliga Fallen för att hålla utställningen så tydlig som möjligt.

När vi försöker modellera effekterna av kovariater (t.ex. Ålder, kön, ras, maskintillverkare) kommer vi vanligtvis att vara intresserade av att förstå effekten av kovariaten på riskfrekvensen. Riskfrekvensen är den momentana sannolikheten för fel/död / statlig övergång vid en given tidpunkt t, beroende på att redan ha överlevt så länge., Vi kommer att beteckna det λ (t). Behandlingstid som diskret:

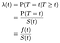
där F är den totala sannolikhetsdensiteten för att misslyckas i tid t. vi kan förena de diskreta och kontinuerliga fallen genom att tillåta deltafunktioner i sannolikhetsdensiteten ”funktion”. Resultatet λ = F/S är således detsamma för det kontinuerliga fallet.

låt oss fixa ett exempel., Låt oss överväga sammanhanget med en klinisk prövning där ett läkemedel initialt orsakar en sjukdom att gå in i remission. Vi kommer att säga att läkemedlet ”misslyckas” för ett ämne när sjukdomen börjar utvecklas för ett ämne. Slutligen anta att försökspersonernas sjukdomsstatuser mäts varje vecka. Sedan Om λ(3) = 0,1, betyder det att det finns en 10% chans att för ett givet ämne, om de fortfarande är i remission före vecka 3, kommer deras sjukdom att börja utvecklas vid vecka 3. De övriga 90% kommer att förbli i remission.,

därefter är den totala sannolikhetsdensitetsfunktionen f bara derivatet av S med avseende på tid. (Återigen, om tiden är diskret, Är f bara summan av vissa deltafunktioner).,341fa8b2″>

det betyder att om vi känner till Farofunktionen kan vi lösa denna differentialekvation för S:

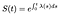
om tiden är diskret blir integralen av summan av deltafunktionerna bara en summa av farorna vid varje diskret tidpunkt.,

okej, det sammanfattar notationen och grundläggande begrepp som vi behöver. Låt oss gå vidare till att diskutera modeller.

icke-, Semi-och helt parametriska modeller

som jag sa tidigare är vi vanligtvis intresserade av att modellera Farofrekvensen λ.

i en icke-parametrisk modell gör vi inga antaganden om den funktionella formen av λ. Kaplan–Meier-kurvan är den maximala Sannolikhetsuppskattaren i detta fall. Nackdelen är att detta gör det svårt att modellera några effekter av kovariater. Det är lite som att använda en scatter plot för att förstå effekten av en kovariat., Inte nödvändigtvis lika bra som en helt parametrisk modell som en linjär regression.

i en helt parametrisk modell gör vi ett antagande för den exakta funktionella formen av λ. En diskussion om de helt parametriska modellerna är en fullständig artikel i sig själv, men det är värt en mycket kort diskussion. Tabellen nedan visar tre av de vanligaste fullt parametriska modellerna. Var och en generaliseras av nästa, går från 1 till 2 till 3 parametrar. Den funktionella formen för farofunktionen visas i mittenkolumnen. Logaritmen för farofunktionen visas också i den sista kolumnen., Alla parametrar (MRL, α, μ) antas vara positiva utom att μ kan vara 0 i den generaliserade Weibullfördelningen (återger Weibullfördelningen).

om man tittar på logaritmen visar att den exponentiella modellen förutsätter att farofunktionen är konstant. Weibull-modellen förutsätter att den ökar om α >1, konstant Om α=1, och minskar om α<1., Den Generaliserade Weibull modellen börjar på samma sätt som Weibull modell (i början ln S = 0). Efter det, en extra term μ sparkar in.

problemet med dessa modeller är att de gör starka antaganden om data. I vissa sammanhang kan det finnas skäl att tro att dessa modeller är en bra passform. Men med dessa och flera andra alternativ finns det en stark risk att dra felaktiga slutsatser på grund av missspecifikation av modellen.

det är därför Cox Proportional Hazards, en halvparametrisk modell är så populär., Inga funktionella antaganden görs om Riskfunktionens form; i stället görs funktionella antaganden om effekterna av kovariaten ensamma.,

modellen för Cox Proportional Hazards

modellen för Cox Proportional Hazards ges vanligtvis när det gäller tid t, kovariatvektor x och koefficientvektor β som

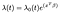
där λ är en godtycklig funktion av tiden, baslinjen fara. Dot-produkten av X och β tas i exponenten precis som i standard linjär regression., Oavsett värden kovariater, alla ämnen har samma baslinje hazard λ. Därefter görs justeringar baserat på kovariaten.

tolkning av resultaten

Antag för ögonblicket att vi har anpassat en Cox proportionell riskmodell till våra data, som bestod av

1. en kolumn som specificerar tiden för varje ämne
2. en kolumn som anger om ämnet ”observerades” (för att ha misslyckats eller, i vårt föredragna exempel, för att få deras sjukdomsframsteg). Ett värde av 1 innebär att ämnet hade sin sjukdomsutveckling., Ett värde på 0 innebär att sjukdomen vid den sista observationstiden inte hade utvecklats. Observationen censurerades.
3. kolumner för våra kovariater X.

efter passformen får vi värden för β. Antag till exempel för enkelhet att det finns en enda kovariat. Ett värde av β=0.1 innebär att en ökning av kovariaten med en mängd av 1 leder till en ungefär 10% hög risk för sjukdomsprogression vid varje given tidpunkt., Det exakta värdet är faktiskt

för små värden av β är värdet av β i sig en ganska bra approximation av den exakta ökningen av faran. För större värden på β måste det exakta beloppet beräknas.

ett annat sätt att uttrycka β=0.1 är att, när x ökar, risken ökar med en hastighet av 10% per ökning av x med 1. Ju större 10.,52% härrör från (kontinuerlig) kompoundering, precis som med sammansatt ränta.

även β = 0 betyder ingen effekt, och β negativ betyder att det finns mindre risk när kovariaten ökar. Observera att, till skillnad från i standardregressioner, finns det ingen avlyssning. Istället absorberas interceptet i baslinjen hazard λ, som också kan uppskattas (se nedan).

slutligen, förutsatt att vi har uppskattat baslinjens farofunktion, kan vi konstruera överlevnadsfunktionen.,

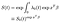
– herr talman! Viss försiktighet bör iakttas vid tolkning av baslinjen överlevande funktion, som grovt spelar rollen av avlyssnings sikt i en regelbunden linjär regression. Om kovariaten har centrerats (medelvärde 0) representerar den överlevnadsfunktionen för det ”genomsnittliga” ämnet.,på 1970-talet föreslog David Cox, en brittisk matematiker, ett sätt att uppskatta β utan att behöva uppskatta utgångsrisken λ. Återigen kan utgångsrisken uppskattas efteråt. Som tidigare nämnts kommer vi att se att det är beställningen av de observerade misslyckanden som är viktiga, inte tiderna själva.

innan du hoppar in i uppskattningen är det värt att diskutera band. Eftersom vi vanligtvis bara observerar data i diskreta steg är det möjligt att två fel kan inträffa samtidigt., Till exempel kan två maskiner misslyckas samma vecka, och inspelningen görs endast varje vecka. Dessa band gör analysen av situationen ganska komplicerad utan att lägga till mycket insikt. Följaktligen kommer jag att härleda uppskattningarna om det inte finns några band.

minns att våra data består av observationer av vissa antal misslyckanden vid diskret tidpunkt. Låt R(t) beteckna befolkningen ”i riskzonen” vid tidpunkten t. om ett ämne i vår studie har misslyckats (sjukdom utvecklats, till exempel) före tid t, är de inte ”i riskzonen.,”Även om ett ämne i vår studie har fått sin observation censurerad vid en tid före t, är de inte heller ”i riskzonen.”

på vanligt sätt vill vi konstruera en sannolikhetsfunktion (vad är sannolikheten att vi skulle ha observerat de data vi gjorde, med tanke på kovariaten och koefficienterna) och sedan optimera det för att få en maximal sannolikhetsuppskattare.

för varje diskret tid när vi observerade ett fel i ämne j, är sannolikheten för att det inträffar, med tanke på att ett fel inträffade, under. Summan tas över alla personer i riskzonen vid tiden j.,

Lägg märke till att baseline hazard λ har hoppat av! Mycket bekvämt. Av denna anledning är sannolikheten att vi konstruerar endast en partiell Sannolikhet. Observera också att tiderna inte visas alls., Termen för ämne j beror endast på vilka ämnen som fortfarande lever vid tiden j, vilket i sin tur bara beror på i vilken ordning ämnena censureras eller observeras misslyckas.

den partiella sannolikheten är naturligtvis bara produkten av dessa villkor, en för varje misslyckande vi observerar (inga villkor för censurerade observationer).,

log partiell sannolikhet är då

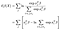
passformen görs med vanliga numeriska metoder, till exempel i pythonpaketet statsmodels och varians-kovariansmatrisen för uppskattningarna ges av (inversen av) Fisher informationsmatrisen. Inget spännande här.,

Estimating the Baseline Survivor Function

Nu när vi har uppskattat koefficienterna kan vi uppskatta överlevnadsfunktionen. Detta slutar vara mycket lik att uppskatta en Kaplan-Meier kurva.

vi postulerar termer α indexeras av i. vid tiden i, baslinjen överlevande kurvan bör minska med en bråkdel α representerar andelen personer i riskzonen som misslyckas vid tiden i., Med andra ord

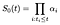
för att beräkna den maximala sannolikhetsuppskattningen för α, anser vi sannolikheten bidrag från subject I som misslyckas vid tiden jag och separat bidraget från dem som censureras vid tiden jag.

för ett ämne som misslyckas vid tiden jag, sannolikheten ges av sannolikheten att de lever vid tiden jag mindre sannolikheten att de lever vid nästa gång jag+1. (Vi antar tillfälligt att tiderna beställs).,

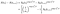
om de istället censureras i tid i, är bidraget bara sannolikheten att de lever vid tiden efter jag, dvs att de inte har dött ännu., Detta är bara

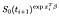
det finns en extra term från de ämnen som observerades (dvs observeras att misslyckas istället för censurerade)., Log sannolikheten blir

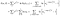
jag har varit lite slarvig om att hålla reda på slutpunkter (i Vs i+1), men det kommer alla att fungera.

det finns bara a villkor för ämnen som vi observerade att misslyckas., Differentiering med avseende på α-j och förutsatt att inga band, får vi ett bidrag från summan till vänster Endast för ämnen som lever vid tiden j, och ett enda bidrag från termen till höger.,Kval till 0 innebär att vi kan få maximal sannolikhet för α Med hjälp av våra uppskattningar för β som lösningen på de flera ekvationerna, en för varje ämne som observerades misslyckas:

figcaption > (ekvation 7) en enkel ekvation att lösa För α uppskattningar

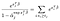
tillägg och varningar

det finns mycket mer att säga om Cox proportionella faror modeller, men jag kommer att försöka hålla saker kort och bara nämna några saker.,

till exempel kan man överväga tidsvarierande regressorer, och detta är möjligt.

den andra avgörande sak att komma ihåg utelämnas variabel bias. I standard linjär regression är utelämnade variabler okorrelerade med regressorerna inte ett stort problem. Detta är inte sant i överlevnadsanalys. Antag att vi har två lika stora och samplade delpopulationer i våra data var och en med en konstant riskhastighet, en är 0.1 och den andra är 0.5. Inledningsvis kommer vi att se en hög riskhastighet (genomsnittet, bara 0,3)., Allteftersom tiden går kommer befolkningen med hög risk att lämna befolkningen och vi kommer att observera en riskhastighet som minskar mot 0.1. Om vi utelämnade variabeln som representerar dessa två populationer kommer vår riskfrekvens att vara helt förstörd.