Pythagoras” sats

Pythagoras

för 2000 år sedan var det en fantastisk upptäckt om trianglar:

När en triangel har en rät vinkel (90°) …

… och kvadrater är gjorda på var och en avtre sidor,…

… då har den största torget exakt samma område som de andra två rutorna tillsammans!,

det kallas ”Pythagoras” teorem” och kan skrivas i en kort ekvation:

a2 + b2 = c2

Obs:

• c är den längsta sidan av triangeln
• a och B är de andra två sidorna

definition

den längsta sidan av triangeln kallas ”hypotenusen”, så den formella definitionen är:

visst … ?

Låt oss se om det verkligen fungerar med ett exempel.

Varför är detta användbart?

om vi känner till längden på två sidor av en rätvinklig triangel kan vi hitta längden på tredje sidan. (Men kom ihåg att det bara fungerar på rätvinkliga trianglar!)

Hur använder jag det?,

skriv ner det som en ekvation:

då använder vi algebra för att hitta något saknat värde, som i dessa exempel:

Du kan också läsa om kvadrater och kvadratiska rötter för att ta reda på varför √169 = 13

det fungerar tvärtom: när de tre sidorna av en triangel gör a2 + b2 = c2, så är triangeln rätt vinklad.,

och du kan bevisa teoremet själv !

hämta papperspenna och sax och använd sedan följande animering som guide:

• rita en rätvinklig triangel på papperet och lämna gott om utrymme.,
• rita en kvadrat längs hypotenusen (den längsta sidan)
• rita samma storlek på andra sidan hypotenusen
• rita linjer som visas på animationen, så här:
• 
• Klipp ut formerna
• ordna dem så att du kan bevisa att den stora torget har samma område som de två rutorna på andra sidor
• rita en kvadrat längs hypotenusen (den längsta sidan)
• rita samma storlek på andra sidan av hypotenusen
• li >

en annan, otroligt enkel, bevis

här är en av de äldsta bevisen att torget på långsidan har samma område som de andra rutorna.,

titta på animationen och var uppmärksam när trianglarna börjar glida runt.

Du kanske vill titta på animeringen några gånger för att förstå vad som händer.

den lila triangeln är den viktiga.

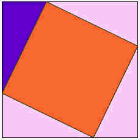blir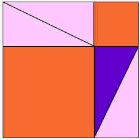