”Jag är övertygad om att han inte kastar tärningar.,”
~ Albert Einstein
- slumpmässiga variabler
- diskreta slumpmässiga variabler
- kontinuerliga slumpmässiga variabler
- blandade slumpmässiga variabler
- kumulativa distributionsfunktioner (CDF)
- Sannolikhetsdensitetsfunktion (PDF)
- interaktivt CDF/PDF-exempel
slumpmässiga variabler:

säg att du skulle ta ett mynt från fickan och kasta det i luften. Medan det vänder genom rymden, vad kan du möjligen säga om dess framtid?
kommer det att landa heads up? Klave?, Mer än så, hur länge kommer det att vara kvar i luften? Hur många gånger kommer det att studsa? Hur långt från där den först träffar marken kommer det äntligen att vila? För den delen, kommer det någonsin att slå i marken? Någonsin kommer att vila?
För vissa sådana frågor, vi kan och gör bosätta sig på svar långt innan observationer; vi är ganska säker gravitation kommer att hålla och myntet kommer att landa. Men för andra har vi inget annat val än att döma och tala mer vagt, om vi vill säga något användbart om framtiden alls.,
som forskare är det naturligtvis vårt jobb att säga något användbart (eller åtminstone auktoritativt…), medan de metaforiska mynten av viktigt fysiskt system fortfarande är i luften. Huvuden eller svansar kan till och med vara en fråga om liv eller död. Våra mynt kan till exempel vara olika möjliga kylvätskeflödeshastigheter eller massor av uran i ett kärnkraftverk. Vi bryr oss mycket om att veta vad våra chanser är att vi kommer att få virvlande turbiner istället för en härdsmälta.,
till en strikt determinist var alla sådana satsningar avgjorda långt innan något mynt, metaforiskt eller inte, någonsin präglades; vi vet helt enkelt inte det. Om vi bara visste de krafter som tillämpas på ett mynt ” s toss, dess exakta fördelning av massa, de olika minutrörelser av luft i rummet… Om vi visste allt det, då skulle vi veta att särskild slantsingling hade en 100% chans att landa som det kommer att landa, och noll chans till något annat resultat.
men vi saknar naturligtvis ofta även en mentionerbar del av sådan kunskap om världen., Dessutom verkar det på mycket små skalor som strikta determinister är helt fel; det finns inget sätt att förutsäga när till exempel en uranatom kommer att delas, och om en sådan händelse påverkar den större världen är den makrohändelsen verkligen oförutsägbar. Vissa resultat är verkligen upp i luften, oroliga tills de är en del av det förflutna.
för att hantera denna verklighet och för att kunna beskriva de framtida tillstånden för ett system på något användbart sätt använder vi slumpmässiga variabler., En slumpmässig variabel är helt enkelt en funktion som relaterar varje möjligt fysiskt utfall av ett system till några unika, verkliga nummer. Som sådan finns det tre typer av slumpmässiga variabler: diskret, kontinuerlig och blandad. I följande avsnitt kommer dessa kategorier att diskuteras kortfattat och exempel kommer att ges.
diskreta slumpmässiga variabler:
överväga vår myntkastning igen. Vi kan ha huvuden eller svansar som möjliga resultat. Om vi definierade en variabel, x, som antalet huvuden i en enda kasta, kan x eventuellt vara 1 eller 0, inget annat., En sådan funktion, x, skulle vara ett exempel på en diskret slumpvariabel. Sådana variabler kan bara ta diskreta värden. Andra exempel skulle vara möjliga resultat av ett graviditetstest, eller antalet studenter i ett klassrum.
kontinuerliga slumpmässiga variabler:
tillbaka till myntet, vad händer om vi ville beskriva avståndet mellan var vårt mynt kom till vila och var det först slog i marken. Det avståndet, x, skulle vara en kontinuerlig slumpmässig variabel eftersom det kan ta ett oändligt antal värden inom det kontinuerliga intervallet av reella tal., Myntet kan resa 1 cm, eller 1,1 cm, eller 1,11 cm, eller på och på. Andra exempel på kontinuerliga slumpmässiga variabler skulle vara massan av stjärnor i vår galax, pH i havsvatten eller uppehållstiden för någon analyt i en gaskromatograf.
blandade slumpmässiga variabler:
blandade slumpmässiga variabler har både diskreta och kontinuerliga komponenter. Sådana slumpmässiga variabler förekommer sällan. För ett möjligt exempel kan du dock mäta ett provs vikt och bestämma att någon vikt som mäts som ett negativt värde kommer att ges ett värde på 0., På så sätt har den slumpmässiga variabeln en diskret komponent vid x = 0 och kontinuerlig komponent där x > 0.
kumulativa distributionsfunktioner (CDF):
frågan uppstår naturligtvis om hur man bäst matematiskt beskriver (och visuellt visar) slumpmässiga variabler. För dessa uppgifter använder vi sannolikhetsdensitetsfunktioner (PDF) och kumulativa densitetsfunktioner (CDF). Eftersom CDFs är enklare att förstå för både diskreta och kontinuerliga slumpmässiga variabler än PDF-filer, kommer vi först att förklara CDFs.
överväga att kasta en rättvis 6-sidded tärningar., Vi skulle ha en 1 i 6 chans att få någon av de möjliga värdena för den slumpmässiga variabeln (1, 2, 3, 4, 5, 6). Om vi plottar de möjliga värdena på X-axeln och plottar sannolikheten för att mäta varje specifikt värde, x eller något värde mindre än x på y-axeln, kommer vi att ha CDF av den slumpmässiga variabeln.
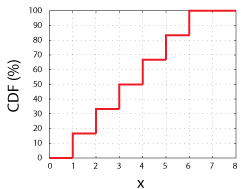
CDF för en rättvis 6-Sidded tärning. Observera att varje steg är en höjd av 16,67%, eller 1 i 6.
denna funktion, CDF(x), berättar helt enkelt oddsen för att mäta något värde upp till och med x., Som sådan måste alla CDFs ha dessa egenskaper:
- en CDF måste vara lika 0 när x = – och approach 1 (eller 100%) som x approaches+. Enkelt uttryckt, av alla möjliga resultat måste det finnas ett resultat; chansen att kasta en sexsidig tärning och få ett värde mellan-och-barbari är 100%.
- lutningen på en CDF måste alltid vara lika med eller större än noll. Tänk till exempel på chansen att kasta en 6-sided tärning (rättvis eller inte) och få ett värde mellan 0 och 4., Den chansen kan inte vara mer än chansen att få ett värde mellan 0 och 5, eftersom oddsen för en 1, 2 eller 3 landning uppåt kommer givetvis alltid att vara en bråkdel av oddsen för att få en 1, 2, 3 eller 4.
för ett exempel på en kontinuerlig slumpvariabel visar följande applet den normalt distribuerade CDF.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., Observera bara att egenskaperna hos en CDF som beskrivs ovan och förklaras för en diskret slumpmässig variabel hold för kontinuerliga slumpmässiga variabler också.
För mer intuitiva exempel på egenskaperna hos CDFs, se det interaktiva exemplet nedan. Dessutom kan interaktiva tomter av många andra CDF-skivor som är viktiga för statistikområdet och används på denna webbplats hittas här.
Sannolikhetsdensitetsfunktioner (PDF):
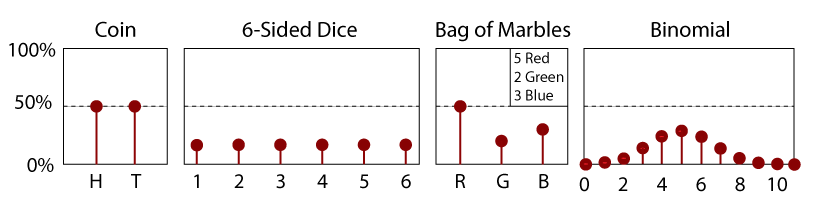
PDF för en rättvis 6-Sidded tärning.
en PDF är helt enkelt ett derivat av en CDF., Således är en PDF också en funktion av en slumpmässig variabel, x, och dess storlek kommer att vara en indikation på den relativa sannolikheten för att mäta ett visst värde. Eftersom det är lutningen på en CDF, måste en PDF alltid vara positiv; det finns inga negativa odds för alla händelser. Vidare och per definition är området under kurvan för en PDF(x) mellan-och x lika med dess CDF(x). Som sådan ger området mellan två värden x1 och x2 sannolikheten att mäta ett värde inom det området.
följande applet visar ett exempel på PDF för en normalt distribuerad slumpvariabel, x.,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
|
|
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., överväga också skillnaden mellan en kontinuerlig och diskret PDF. Medan en diskret PDF (som det som visas ovan för tärningar) ger dig oddsen att få ett visst resultat, är sannolikheter med kontinuerliga PDF-filer frågor om intervall, inte diskreta punkter. Till exempel finns det tydligt en 1 i 6 (16.6%) chans att rulla en 3 på en tärning, vilket kan ses i sin PDF. Men vad är det udda att mäta exakt noll med en slumpmässig variabel som har en normal PDF och medelvärde på noll, som visas ovan? Även om det är det värde där PDF är störst, chansen att mäta exakt 0.00000..,. är, kanske räknare intuitivt, noll. Oddsen att mäta ett visst slumptal ut till oändlig precision är i själva verket noll. med en kontinuerlig PDF kan du istället fråga vad oddsen är att du kommer att mäta mellan två värden för att få en sannolikhet som är större än noll. För att hitta denna sannolikhet använder vi helt enkelt CDF i vår slumpmässiga variabel., Eftersom CDF berättar det udda att mäta ett värde eller något lägre än det värdet, för att hitta sannolikheten för att mäta mellan två värden, x1 och x2 (där x1 > x2), måste vi helt enkelt ta värdet av CDF vid x1 och subtrahera från det värdet av CDF vid x2. Till exempel, med den normala CDF i appleten ovan (med μ=0 och σ=1), Om vi ville veta oddsen att mäta mellan 0,01 och 0,02 hittar vi CDF(x=0,1)=53,9828% och CDF(x=0,2)=57,9260%. Då ger skillnaden, CDF(0.2)-CDF (0.1), oss oddsen på ca 3.9% för att mäta en x mellan 0.1 och 0.2., För mer intuitiva, visuella exempel på egenskaperna hos PDF-filer, se det interaktiva exemplet nedan. Också, interaktiva tomter av många viktiga PDF-filer som används på denna webbplats kan ses här. |
|||||||||||||||||