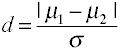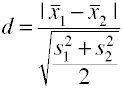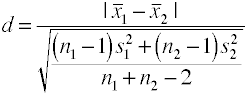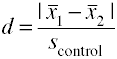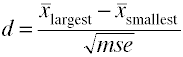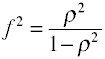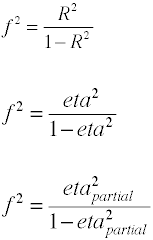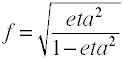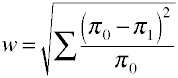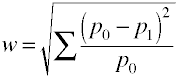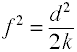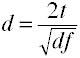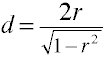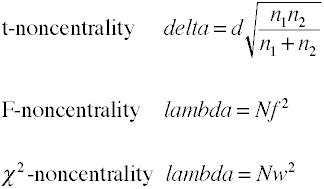Eine Verwendung der Effektgröße ist ein standardisierter Index, der unabhängig von der Stichprobengröße ist und die Größe der Differenz zwischen Populationen oder die Beziehung zwischen erklärenden und Antwortvariablen quantifiziert. Eine andere Verwendung der Effektgröße ist ihre Verwendung bei der Durchführungpower-Analyse.
Wirkung Größe für Unterschied in Mittel
der effektgröße für Unterschiede in bedeutet, ist gegeben byCohen d ist definiert in Bezug auf die Bevölkerung bedeutet (µs) und einer Bevölkerung standarddeviation (σ), wie unten gezeigt.,
Es gibt verschiedene Möglichkeiten, σ aus Beispieldaten zu schätzen, dieführt zu mehreren Varianten innerhalb der Cohen-d-Familie.
Unter Verwendung der Standardabweichung root mean square Standardabweichung
Unter Verwendung der gepoolten Standardabweichung (Hedges‘ g)
Diese Version von Cohens d verwendet die gepoolte Standardabweichung und wird auch als Hedges‘ g bezeichnet.,
Sie können diesen Wert ganz einfach aus einem Anova-Programm abrufen, indem Sie die Quadratwurzel des Meansquare-Fehlers verwenden, der auch als root Mean Square-Fehler bezeichnet wird.
Unter Verwendung der Standardabweichung der Kontrollgruppe (Glas‘ Δ)
Eine andere Version von Cohens d unter Verwendung der Standardabweichung für die Kontrollgruppe wird auch als Glas‘ Δ bezeichnet.,
Mehr als zwei Gruppen
Wenn es mehr als zwei Gruppen gibt, verwenden Sie den Unterschied zwischen dem größten und dem kleinstenmittel geteilt durch die Quadratwurzel des mittleren Quadratfehlers.
Effektgröße für F-Verhältnisse in der Regressionsanalyse
Für OLS-Regression Das Maß der Effektgröße ist F, das von Cohen wie folgt definiert wird.,
Erneut gibt es mehrere Möglichkeiten, die Effektgröße aus Beispieldaten zu berechnen. Beachtendass η2 ist ein anderer name für R2.
Effektgröße für F-Verhältnisse bei der Varianzanalyse
Die bei der Varianzanalyse verwendete Effektgröße wird durch das Verhältnis der Populationsstandardbewertungen definiert.,
Obwohl Cohens f wie oben definiert ist, wird es normalerweise berechnet, indem die Quadratwurzel von f2 verwendet wird.
Effektstärke für χ2 from contingency tables
wieder Einmal beginnen wir mit der definitorischen Formel in Bezug auf die Bevölkerung-Werte.Effektgröße w ist die Quadratwurzel der standardisierten Chi-Quadrat-Statistik.,
Und so wird w mit Beispieldaten berechnet.
Hier ist eine Tabelle der empfohlenen Werte für niedrige, mittlere und hohe Effekte (nach Cohen, 1988). Diese Werte sollten nicht als absolut betrachtet und im Rahmen Ihres Forschungsprogramms interpretiert werden. In der Praxis werden die Grenzwerte für Stickoxide in der Praxis häufig überschritten, Werte über 1,0 sind keine Seltenheit.,Die Verwendung sehr großer Effektgrößen in der prospektiven Leistungsanalyse ist jedoch wahrscheinlich keine gute Idee, da dies zu unterversorgten Studien führen könnte.,formeln
wobei k = Anzahl der Gruppen
Konvertieren Sie t in d für zwei unabhängige Gruppen
Konvertieren von r nach d für zwei unabhängige Gruppen
Nichtzentralitätsschätzungen
Die Leistungsanalyse mit Analysemethoden erfordert eine Schätzung der Nichtzentralität, die ist im Grunde die Effektgröße multipliziert mit einem Stichprobengrößenfaktor., Hier sind einige Formeln zur Schätzung der Nichtzentralität.
Beispiel Leistungsanalyse
Hier ist ein Beispiel, das Effektgröße und Nichtzentralität in einer Leistungsanalyse zusammenbringt.
Betrachten Sie eine Einweg-Varianzanalyse mit drei Gruppen (k = 3). Wenn wir andeta2 gleich erwarten .,12 in diesem Fall beträgt die Effektgröße
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
Bei einer projizierten Stichprobengröße von 60 beträgt die Schätzung der Nichtzentralität
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
Die Freiheitsgrade des Zählers sind k-1 = 3-1 = 2, während der Nenner df N-k = 60-3 = 57 ist.Der kritische Wert von F mit 2 und 57 Freiheitsgraden beträgt 3,16. Dies führt zu einer Potenz von
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
somit zu einem N von 60 und einer Effektgröße von .369 ergibt eine projizierte Leistung von etwa .7.
Wir können verbessern auf die power von .7 durch Verwendung einer projizierten Stichprobengröße von 75 statt 60., Mit der gleichen Effektgröße von.369 erhalten wir eine neue Nichtzentralitätsschätzung von
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
Die Freiheitsgrade des Zählers bleiben gleich, während der Nenner jetzt gleich ist N-k = 75-3 = 72.Der kritische Wert von F mit 2 und 72 Freiheitsgraden von 3.12. Diesmal ist die Leistung
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
, was innerhalb akzeptabler Forschungsgrenzen liegt.
Bitte beachten Sie, dass verschiedene stat-Pakete unterschiedliche Namen und eine andere Reihenfolge von Argumenten in der Funktion verwenden, die wir noncentralFtail. Sie müssen die Dokumentation lesen, diekommt mit Ihrer Software.,
Becker, L. Psychologie 590 Kurs Notizen. Gesehen 19 Jun 2009 <http://web.uccs.edu/lbecker/Psy590/es.htm>
Cohen, J. 1988. Statistische Leistungsanalyse für die Verhaltenswissenschaften. Hillsdale, New Jersey:Lawrence Erlbaum Associates