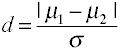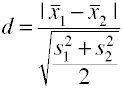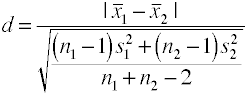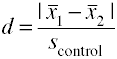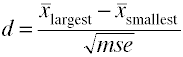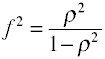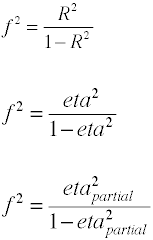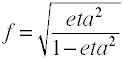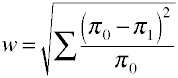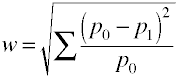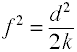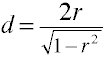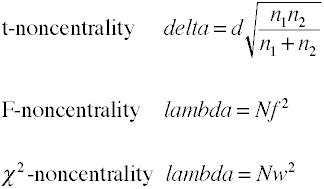jednym z zastosowań rozmiaru efektu jest znormalizowany indeks, który jest niezależny od wielkości próby i określa wielkość różnicy między populacjami lub związek między zmiennymi objaśniającymi i odpowiedziowymi. Innym zastosowaniem wielkości efektu jest jego zastosowanie w przeprowadzaniu analizy mocy.
wielkość efektu dla różnic w średnich
wielkość efektu dla różnic w średnich jest podana przez D jest zdefiniowana w kategoriach średniej populacji (µs) i standardu populacji (σ), Jak pokazano poniżej.,
istnieje kilka różnych sposobów, które można oszacować σ na podstawie przykładowych danych, które prowadzą do wielu wariantów w obrębie rodziny D Cohena.
używając podstawowego średniego kwadratowego odchylenia standardowego
używając łącznego odchylenia standardowego (Hedges' g)
Ta wersja Cohena d używa zbiorcze odchylenie standardowe i jest również znany jako Hedges' g.,
możesz łatwo uzyskać tę wartość z programu anova, pobierając pierwiastek kwadratowy błędu meansquare, który jest również znany jako średni błąd kwadratowy.
stosując odchylenie standardowe grupy kontrolnej (Glass' Δ)
inna wersja d Cohena wykorzystująca odchylenie standardowe dla grupy kontrolnej jest również znana jako glass' Δ.,
więcej niż dwie grupy
gdy jest więcej niż dwie grupy, użyj różnicy między największymi i najmniejszymi znacznikami podzielonymi przez pierwiastek kwadratowy średniego błędu kwadratowego.
wielkość efektu dla współczynników F w analizie regresji
dla regresji OLS miarą wielkości efektu jest F, która jest zdefiniowana przez Cohena w następujący sposób.,
Po raz kolejny istnieje kilka sposobów obliczania rozmiaru efektu na podstawie przykładowych danych. Uwaga: η2 to inna nazwa dla R2.
Rozmiar efektu dla współczynników F w analizie wariancji
rozmiar efektu stosowany w analizie wariancji jest zdefiniowany przez współczynnik norm populacji.,
chociaż f Cohena jest zdefiniowany jak powyżej, zwykle jest obliczany przez pobranie pierwiastka kwadratowego f2.
Rozmiar efektu dla χ2 z tabel interwencyjnych
Po raz kolejny zaczynamy od formuły definicyjnej pod względem wartości populacji.Rozmiar efektu w jest pierwiastkiem kwadratowym znormalizowanej statystyki chi-kwadrat.,
a oto jak w jest obliczany przy użyciu przykładowych danych.
oto tabela sugerowanych wartości dla niskich, średnich i wysokich efektów (Cohen, 1988). Wartości te nie powinny być traktowane jako absolutne i powinny być interpretowane w kontekście programu badawczego. W praktyce często przekraczane są wartości D większe niż 1,0.,Jednak stosowanie bardzo dużych rozmiarów efektów w prospektywnej analizie mocy prawdopodobnie nie jest dobrym pomysłem, ponieważ może prowadzić do badań pod mocą.,formuły
gdzie k = liczba grup
Konwertuj t na d dla dwóch niezależnych grup
iv id=”309893e07b”
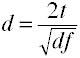
konwersja r NA D dla dwóch niezależnych grup
szacunki niecentralności
analiza mocy przy użyciu metod analitycznych wymaga oszacowania niecentralności, która jest zasadniczo wielkością efektu pomnożoną przez współczynnik wielkości próbki., Oto kilka wzorów na oszacowanie niecentralności.
przykładowa analiza mocy
oto przykład, który łączy rozmiar efektu i niecentralność w analizie mocy.
rozważmy jednokierunkową analizę wariancji z trzema grupami (k = 3). Jeśli spodziewamy się, że andeta2 będzie równy .,12 W takim przypadku rozmiar efektu będzie
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
przy projektowanej wielkości próbki 60 oszacowanie niezgodności wynosi
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
stopni swobody licznika wynosi k-1 = 3-1 = 2, podczas gdy mianownik df wynosi N-k = 60-3 = 57.Wartość krytyczna F z 2 i 57 stopniami swobody wynosi 3,16. Co daje moc
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
tak więc N wynosi 60 i wielkość efektu .369 daje przewidywaną moc ok .7.
możemy poprawić moc .7 poprzez zastosowanie przewidywanego rozmiaru próby 75 zamiast 60., Z tym samym rozmiarem efektu.369, otrzymujemy nowe oszacowanie niecentralności
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
stopnie swobody licznika pozostają takie same, podczas gdy mianownik df wynosi teraz N-k = 75-3 = 72.Wartość krytyczna F z 2 i 72 stopniami swobody 3.12. Tym razem moc jest
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
, która mieści się w dopuszczalnych granicach badań.
należy pamiętać, że różne pakiety stat używają różnych nazw i innej kolejności argumentów w funkcji, którą nazywamy noncentralFtail. Będziesz musiał przeczytać dokumentację, któraznika się z oprogramowaniem.,
Obejrzano 19 Cze 2009 <http://web.uccs.edu/lbecker/Psy590/es.htm>
Statystyczna analiza mocy dla nauk behawioralnych. Hillsdale, New Jersey: Lawrence Erlbaum Associates