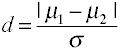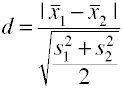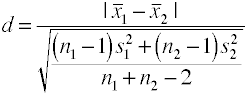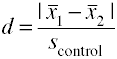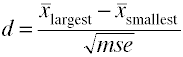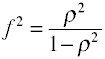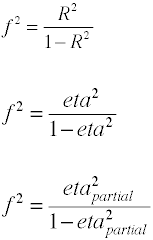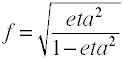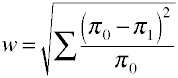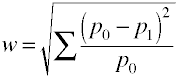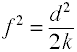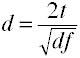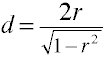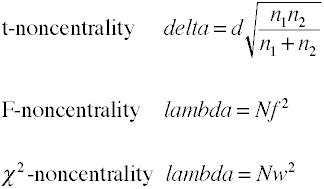en användning av effektstorlek är som ett standardiserat index som är oberoende av provstorlek och kvantifierar storleken på skillnaden mellan populationer eller förhållandet mellan förklarande och svarvariabler. En annan användning av effektstorlek är dess användning vid utförandeströmanalys.
effektstorlek för skillnad i medel
effektstorlek för skillnader i medel ges bycohens d definieras i termer av populationsorgan (µs) och en populationsstandarddeviation (σ), som visas nedan.,
det finns flera olika sätt att uppskatta σ från provdata som leder till flera varianter inom Cohens d-familj.
använda standardavvikelsen root mean square
använda den sammanslagna standardavvikelsen (häckar’ g)
den här versionen av Cohens d använder den sammanslagna standardavvikelsen och kallas även häckar’ g.,
Du kan enkelt få detta värde från ett anova-program genom att ta kvadratroten av meansquare-felet som också är känt som root mean square-felet.
användning av kontrollgruppens standardavvikelse (glas’ Δ)
en annan version av Cohens d med hjälp av standardavvikelsen för kontrollgruppen är också känd somglas ’ Δ.,
mer än två grupper
När det finns fler än två grupper använder skillnaden mellan de största och minstabetyder dividerat med kvadratroten av mean square-felet.
effektstorlek för F-förhållanden i regressionsanalys
för OLS-regression är måttet på effektstorleken F som definieras av Cohen enligt följande.,
det finns flera sätt på vilka effektstorleken kan beräknas från provdata. Notethat η2 är ett annat namn för R2.
effektstorlek för F-förhållanden vid analys av varians
effektstorleken som används vid analys av varians definieras av förhållandet mellan populationsstandardavvikelser.,
Även om Cohens f definieras som ovan beräknas det vanligtvis genom att ta kvadratroten av f2.
effektstorlek för χ2 från beredskapstabeller
än en gång börjar vi med definitionsformeln när det gäller befolkningsvärden.Effektstorlek w är kvadratroten av den standardiserade chi-kvadratiska statistiken.,
och här är hur w beräknas med hjälp av exempeldata.
här är en tabell med föreslagna värden för låga, medelstora och höga effekter (Cohen, 1988). Dessa värden bör inte tas som absoluta och bör tolkas inom ramen för ditt forskningsprogram. Värdena förstora effekter överskrids ofta i praktiken med värden Cohens d större än 1,0 inte ovanligt.,Men att använda mycket stora effektstorlekar i prospektiv kraftanalys är förmodligen inte en bra idé, eftersom det kan leda till underdrivna studier.,formler
där k = antal grupper
konvertera t till d för två oberoende grupper
konvertera r till D för två oberoende grupper
uppskattning av icke-excentralitet som är grundläggandeeffektstorleken multiplicerad med en provstorleksfaktor., Här är några formler för att uppskatta noncentrality.
exempel på strömanalys
här är ett exempel som sammanför effektstorlek och icke-excentralitet i en kraftanalys.
överväga en enkelriktad analys av varians med tre grupper (k = 3). Om vi förväntar oss andeta2 till Lika .,12 i vilket fall effektstorleken kommer att vara
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
med en projicerad provstorlek på 60 är uppskattningen av icke-excentralitet
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
täljarens frihetsgrader K-1 = 3-1 = 2 medan nämnaren df är N-k = 60-3 = 57.Det kritiska värdet av F med 2 och 57 grader av frihet är 3.16. Vilket resulterar i en effekt på
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
således en n av 60 och effektstorlek på .369 ger en projicerad kraft på ungefär .7.
vi kan förbättra kraften i .7 genom att använda en projicerad provstorlek på 75 istället för 60., Med samma effekt storlek.369, vi får en ny icke-excentralitets uppskattning av
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
täljaren frihetsgrader förblir densamma medan nämnaren DF nu lika N-k = 75-3 = 72.Det kritiska värdet av F med 2 och 72 grader av frihet 3.12. Den här gången är strömmen
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
som ligger inom acceptabla forskningsgränser.
Observera att olika stat-paket använder olika namn och en annan ordning av argument ifunktionen som vi har kallar noncentralFtail. Du måste läsa dokumentationen somkommer med din programvara.,
Becker, L. Psykologi 590 kursanteckningar. Sedd 19 Jun 2009 <http://web.uccs.edu/lbecker/Psy590/es.htm>
Cohen, J. 1988. Statistisk kraftanalys för beteendevetenskap. Hillsdale, New Jersey:Lawrence Erlbaum Associates