spændinger & afbøjninger i bjælker

forskydningskraft og bøjningsmoment

for at finde forskydningskraften og bøjningsmomentet over længden af en bjælke skal du først løse for de eksterne reaktioner ved grænsebetingelserne., For eksempel, cantilever stråle nedenfor er en kraft, der er vist i rødt, og de reaktioner, der er vist i blå til den faste grænse tilstand:

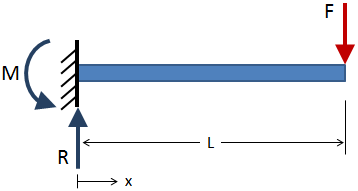
Efter at den eksterne reaktioner, er blevet løst til at tage del snit langs længden af bjælken og løse for reaktioner på hvert udsnit. Et eksempel sektion snit er vist i nedenstående figur:

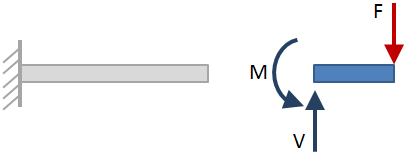
når strålen skæres i sektionen, kan hver side af strålen overvejes, når man løser for reaktionerne., Den valgte side påvirker ikke resultaterne, så vælg hvilken side der er nemmest. I figuren ovenfor blev siden af bjælken til højre for sektionen skåret valgt. Reaktionerne ved snittet vises med blå pile.

tegn konvention

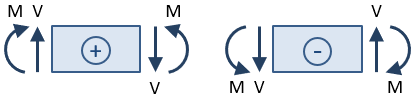
tegnene på forskydningen og øjeblikket er vigtige. Tegnet bestemmes efter en sektion snit er taget, og reaktionerne er løst for den del af strålen til den ene side af snittet., Forskydningskraften ved sektionsskæringen betragtes som positiv, hvis den forårsager rotation med uret af den valgte bjælkesektion, og den betragtes som negativ, hvis den forårsager rotation mod uret. Bøjningsmomentet ved sektionsskæringen betragtes som positivt, hvis det komprimerer toppen af bjælken og forlænger bunden af bjælken (dvs.hvis det får bjælken til at “smile”).

baseret på denne tegnkonvention er forskydningskraften ved det afsnit, der er skåret i figuren ovenfor, positiv, da det forårsager rotation med uret af det valgte afsnit., Øjeblikket er negativt, da det komprimerer bunden af bjælken og forlænger toppen (dvs.det gør bjælken “rynket”).

Forskydning og Moment Diagrammer

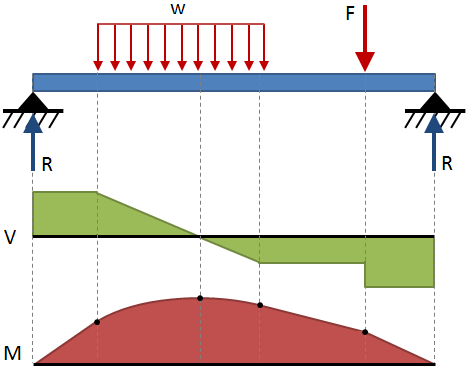
shear og bøjende moment på hele en stråle er ofte udtrykt med diagrammer. Et forskydningsdiagram viser forskydningen langs bjælkens længde, og et momentdiagram viser bøjningsmomentet langs bjælkens længde., Disse diagrammer er typisk vist stablet oven på hinanden, og kombinationen af disse to diagrammer er en shear-moment diagram. Forskydningsmomentdiagrammer for nogle almindelige slutbetingelser og indlæsningskonfigurationer vises i strålebøjningstabellerne i slutningen af denne side., Et eksempel på et shear-øjeblik diagram er vist i følgende figur:

Generelle regler for tegning shear-øjeblik diagrammer er givet i tabellen nedenfor:

Shear Diagram

Øjeblik Diagram

Punkt belastninger forårsage et lodret hop i shear diagram. Hoppets retning er den samme som tegn på punktbelastningen. ensartede fordelte belastninger resulterer i en lige, skrånende linje på forskydningsdiagrammet., Linjens hældning er lig med værdien af den fordelte belastning. forskydningsdiagrammet er vandret for afstande langs bjælken uden påført belastning. shear på ethvert punkt langs bjælken er lig med hældningen på det tidspunkt, på det samme tidspunkt:

i Det øjeblik tegningen er en lige, skrå linje for afstande langs strålen med ikke anvendes belastning. Linjens hældning er lig med forskydningens værdi., ensartede fordelte belastninger resulterer i en parabolsk kurve på momentdiagrammet. de maksimale / minimale værdier for moment forekommer, hvor forskydningslinjen krydser nul. i Det øjeblik, på et givet punkt langs bjælken er lig med arealet under shear-diagram til at: M = ∫ V dx

Bøjning Understreger i Bjælker

Det bøjende moment, M, langs længden af bjælken kan bestemmes ud fra det øjeblik tegningen., Bøjningsmomentet på ethvert sted langs bjælken kan derefter bruges til at beregne bøjningsspændingen over bjælken”s tværsnit på det sted., Det bøjende moment, der varierer over højden af tværsnittet i henhold til bøjning formlen nedenfor:

hvor M er det bøjende moment på placeringen af interesse langs bjælken”s længde, Ic er centroidal inertimoment af bjælken”s tværsnit, og y er afstanden fra bjælken”s neutrale akse til det punkt af interesse sammen højden af tværsnittet. Det negative tegn indikerer, at et positivt øjeblik vil resultere i en trykspænding over den neutrale akse.,

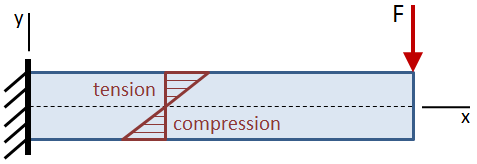
bøjning stress er nul ved strålen”s neutral akse, som er sammenfaldende med centroid af strålen”s tværsnit. Bøjningsspændingen øges lineært væk fra den neutrale akse indtil de maksimale værdier ved de ekstreme fibre øverst og nederst på bjælken.

Den maksimale bøjning stress er givet ved:

hvor c er det centroidal afstand af tværsnit (afstanden fra barycentrum til det yderste fibre).,

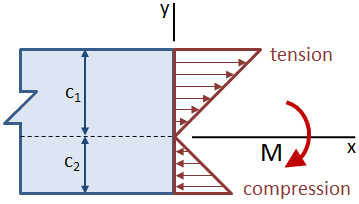
hvis strålen er asymmetrisk omkring den neutrale akse, således at afstandene fra den neutrale akse til toppen og til bunden af bjælken ikke er ens, vil den maksimale spænding forekomme på det fjerneste sted fra den neutrale akse. I figuren nedenfor er trækspændingen øverst på bjælken større end trykspændingen i bunden.,

afsnit modulus af et tværsnit kombinerer centroidal inertimoment, Ic -, og centroidal afstand, c:

gavn af afsnit modul er, at det kendetegner modstandsdygtighed over for bøjning af et tværsnit i et enkelt udtryk., Afsnittet modul kan blive indskiftet i den bøjning formel til at beregne den maksimale bøjning stress i et tværsnit:

Shear stress i Bjælker

shear force, V, langs længden af bjælken kan bestemmes ud fra shear diagram. Forskydningskraften på ethvert sted langs bjælken kan derefter bruges til at beregne forskydningsspændingen over bjælken”s tværsnit på det sted., Den gennemsnitlige shear stress over tværsnittet er givet ved:

shear stress varierer over højden af tværsnittet, som vist i nedenstående figur:

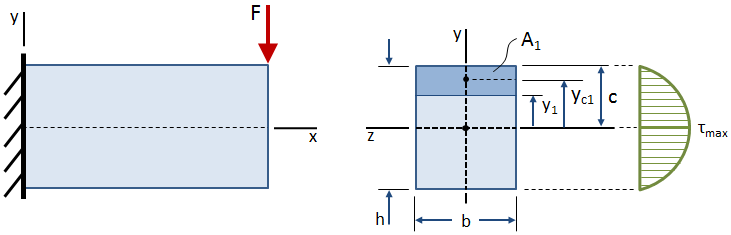
shear stress er nul på den frie overflader (toppen og bunden af bjælken), og det er højst på barycentrum., Ligningen for shear stress på ethvert punkt, som ligger i en afstand y1 fra barycentrum af tværsnittet er givet ved:

hvor V er shear kraft, der virker ved placering af tværsnit, Ic er centroidal inertimoment af tværsnit, og b er bredden på tværs af afsnit. Disse vilkår er alle konstanter., Term-udtrykket er det første øjeblik i området afgrænset af interessepunktet og den ekstreme fiber i tværsnittet:

forskydningsspændinger for flere almindelige tværsnit diskuteres i afsnittene nedenfor.,t af området på et givet punkt y1 langs højden af tværsnittet er beregnet ved:

Den maksimale værdi af Q opstår ved den neutrale akse stråle (hvor y1 = 0):

shear stress på ethvert givet punkt y1 langs højden af tværsnittet er beregnet ved:

hvor Ic = b·h3/12 er centroidal inertimoment af tværsnit., Den maksimale forskydningsspænding opstår ved den neutrale akse stråle og er beregnet ved:

hvor A = b·h er det område af tværsnit.

Bemærk, at den maksimale forskydningsspænding i tværsnittet er 50% højere end den gennemsnitlige belastning V / A.,

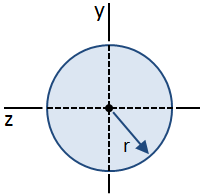
Shear Understreger i Cirkulære Afsnit

Et cirkulært tværsnit er vist i figuren nedenfor:

ligninger for shear stress i en stråle, der blev udledt ved hjælp af den antagelse, at den forskydningsspænding langs bredden af bjælken er konstant. Denne antagelse Gælder ved centroid af et cirkulært tværsnit, selvom det ikke er gyldigt andre steder., Derfor, mens fordelingen af forskydningsspænding langs tværsnittets højde ikke let kan bestemmes, kan den maksimale forskydningsspænding i sektionen (forekommer ved centroid) stadig beregnes., Den maksimale værdi af første øjeblik, Q, som opstår på barycentrum, er givet ved:

Den maksimale forskydningsspænding er derefter beregnet ved:

hvor b = 2r er diameteren (bredde) af tværsnit, Ic = nr4/4 er centroidal inertimoment, og A = nr2 er det område af tværsnit.,t, Q, som opstår på barycentrum, er givet ved:

Den maksimale forskydningsspænding er derefter beregnet ved:

Shear stress i I-Bjælker

fordelingen af forskydningsspænding langs web af en i-Bjælke er vist i nedenstående figur:

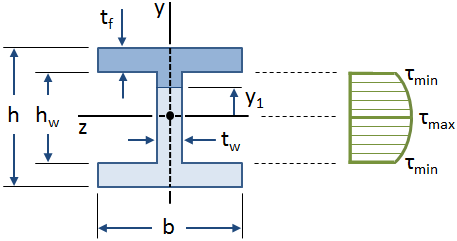
ligninger for shear stress i en stråle, der blev udledt ved hjælp af den antagelse, at den forskydningsspænding langs bredden af bjælken er konstant., Denne antagelse er gyldig over nettet af en I-stråle, men den er ugyldig for flangerne (specifikt hvor banen skærer flangerne). 90% – 98%, ifølge Gere), og det kan derfor konservativt antages, at nettet bærer hele forskydningskraften.,>

Den maksimale værdi af shear stress opstår ved den neutrale akse ( y1 &lig med; 0 ), og den mindste værdi af shear stress i web opstår ved de ydre fibre af internettet, hvor den skærer flangerne y1 &lig; ±hw/2 ):

Bjælke Deformation Tabeller

tabellerne nedenfor giver ligninger for nedbøjning, hældning, shear, og øjeblik sammen lige bjælker til forskellige formål betingelser og belastninger. Du kan finde omfattende tabeller i referencer som Gere, Lindeburg og Shigley., Tabellerne nedenfor dækker dog de fleste af de almindelige tilfælde.

Cantilever Bjælker

simpelt Understøttede Bjælker

fast-Fast Bjælker