Scherkraft und Biegemoment
Um die Scherkraft und das Biegemoment über die Länge eines Balkens zu ermitteln, suchen Sie zunächst nach den äußeren Reaktionen bei den Randbedingungen., Zum Beispiel hat der freitragende Strahl unten eine aufgebrachte Kraft, die in rot gezeigt wird, und die Reaktionen werden in blau an der festen Randbedingung gezeigt:
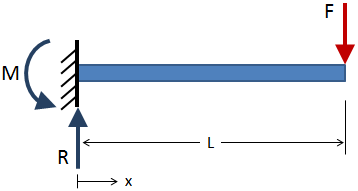
Nachdem die externen Reaktionen gelöst wurden, nehmen Sie Abschnittsschnitte entlang der Länge des Strahls und lösen Sie für die Reaktionen an jedem Schnittabschnitt. Ein Beispiel für den Schnitt des Abschnitts ist in der folgenden Abbildung dargestellt:
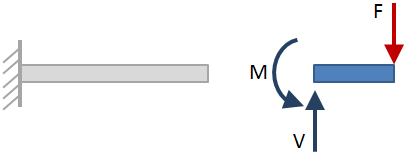
Wenn der Strahl am Abschnitt geschnitten wird, kann bei der Lösung für die Reaktionen jede Seite des Strahls berücksichtigt werden., Die ausgewählte Seite hat keinen Einfluss auf die Ergebnisse, also wählen Sie die Seite, die am einfachsten ist. In der obigen Abbildung wurde die Seite des Balkens rechts vom Schnittschnitt ausgewählt. Die Reaktionen im Schnitt sind mit blauen Pfeilen dargestellt.
Vorzeichenkonvention
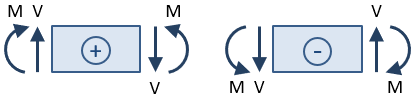
Die Vorzeichen der Scherung und des Moments sind wichtig. Das Vorzeichen wird bestimmt, nachdem ein Schnittschnitt genommen wurde und die Reaktionen für den Teil des Strahls zu einer Seite des Schnittes gelöst sind., Die Scherkraft am Schnittschnitt wird als positiv angesehen, wenn sie eine Drehung des ausgewählten Strahlabschnitts im Uhrzeigersinn bewirkt, und sie wird als negativ angesehen, wenn sie eine Drehung gegen den Uhrzeigersinn bewirkt. Das Biegemoment am Schnittschnitt gilt als positiv, wenn es die Oberseite des Balkens komprimiert und die Unterseite des Balkens verlängert (d. H. Wenn der Balken „lächelt“).
Basierend auf dieser Vorzeichenkonvention ist die Scherkraft am Schnittabschnitt in der obigen Abbildung positiv, da sie eine Drehung des ausgewählten Abschnitts im Uhrzeigersinn bewirkt., Das Moment ist negativ, da es die Unterseite des Balkens komprimiert und die Oberseite verlängert (d. H. Es macht den Balken „stirnrunzeln“).
Schauen Sie sich unseren Strahlrechner an, der auf der hier beschriebenen Methodik basiert.,
- Berechnet Spannungen und Durchbiegungen in geraden Balken
- Erstellt Scher-und Momentendiagramme
- Kann jede Konfiguration von Einschränkungen, konzentrierten Kräften und verteilten Kräften angeben

Scher-und Momentendiagramme
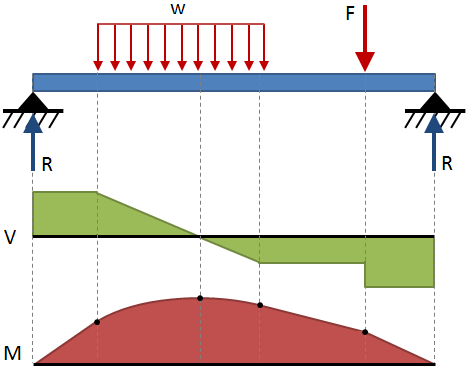
Das Scher-und Biegemoment in einem Strahl wird üblicherweise mit Diagrammen ausgedrückt. Ein Scherdiagramm zeigt die Scherung entlang der Länge des Balkens und ein Momentdiagramm zeigt das Biegemoment entlang der Länge des Balkens., Diese Diagramme werden typischerweise übereinander gestapelt dargestellt, und die Kombination dieser beiden Diagramme ist ein Schermomentdiagramm. Schermomentdiagramme für einige gängige Endbedingungen und Belastungskonfigurationen werden in den Strahlumlenkungstabellen am Ende dieser Seite angezeigt., Ein Beispiel für ein Schermomentdiagramm ist in der folgenden Abbildung dargestellt:
In der folgenden Tabelle sind allgemeine Regeln für das Zeichnen von Schermomentdiagrammen angegeben:
| Scherdiagramm | Momentdiagramm |
|---|---|
|
|
Biegespannungen in Balken
Das Biegemoment M entlang der Länge des Balkens kann aus dem Momentendiagramm bestimmt werden., Das Biegemoment an einer beliebigen Stelle entlang des Trägers kann dann verwendet werden, um die Biegespannung über den Querschnitt des Trägers an dieser Stelle zu berechnen., Das Biegemoment variiert über die Höhe des Querschnitts gemäß der folgenden Biegeformel:
wobei M das Biegemoment an der interessierenden Stelle entlang der Länge des Strahls ist, Ic das zentroidale Trägheitsmoment des Querschnitts des Strahls ist und y der Abstand von der neutralen Achse des Strahls ist.zum Punkt von Interesse entlang der Höhe des Querschnitts. Das negative Vorzeichen zeigt an, dass ein positives Moment zu einer Druckspannung über der Neutralachse führt.,
Die Biegespannung ist an der Neutralachse des Trägers Null, was mit dem Schwerpunkt des Querschnitts des Trägers übereinstimmt. Die Biegespannung steigt linear von der Neutralachse weg bis zu den Maximalwerten an den Extremfasern oben und unten am Träger.
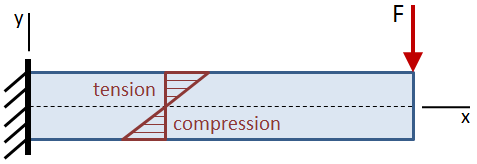
Die maximale Biegebeanspruchung ist gegeben durch:
wobei c der zentroidale Abstand des Querschnitts ist (der Abstand des Querschnitts vom Mittelpunkt bis zur extremen Faser).,
Wenn der Strahl um die Neutralachse asymmetrisch ist, so dass die Abstände von der Neutralachse zur Ober-und Unterseite des Strahls nicht gleich sind, tritt die maximale Spannung an der entferntesten Stelle von der Neutralachse auf. In der folgenden Abbildung ist die Zugspannung an der Oberseite des Balkens größer als die Druckspannung an der Unterseite.,
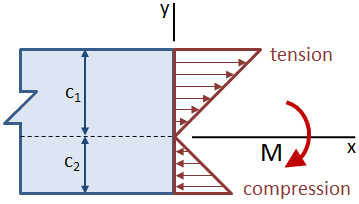
Der Schnittmodul eines Querschnitts kombiniert das zentroidale Trägheitsmoment, Ic und den zentroidalen Abstand, c:
Der Vorteil des Schnittmoduls besteht darin, dass er die Biegefestigkeit eines Querschnitts in einem einzigen Term charakterisiert., Der Schnittmodul kann in die Biegeformel eingefügt werden, um die maximale Biegespannung in einem Querschnitt zu berechnen:
Schauen Sie sich unseren Strahlrechner an, der auf der hier beschriebenen Methodik basiert.,
- Berechnet Spannungen und Auslenkungen in geraden Balken
- Erstellt Scher-und Momentdiagramme
- Kann jede Konfiguration von Einschränkungen, konzentrierten Kräften und verteilten Kräften angeben

Scherspannungen in Balken
Die Scherkraft, V, entlang der Länge des Balkens kann aus dem Scherdiagramm bestimmt werden. Die Scherkraft an einer beliebigen Stelle entlang des Balkens kann dann verwendet werden, um die Scherspannung über den Querschnitt des Balkens an dieser Stelle zu berechnen., Die durchschnittliche Scherspannung über den Querschnitt ist gegeben durch:
Die Scherspannung variiert über die Höhe des Querschnitts, wie in der folgenden Abbildung gezeigt:
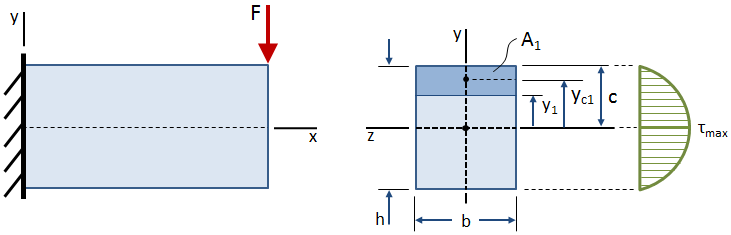
Die Scherspannung ist an den freien Flächen (Ober-und Unterseite des Balkens) Null und am Schwerpunkt maximal., Die Gleichung für die Scherspannung an einem beliebigen Punkt in einem Abstand y1 vom Schwerpunkt des Querschnitts ist gegeben durch:
wobei V die Scherkraft ist, die an der Stelle des Querschnitts wirkt, Ic das zentroidale Trägheitsmoment des Querschnitts ist und b die Breite des Querschnitts ist. Diese Begriffe sind alle Konstanten., Der Q-Term ist der erste Moment des Bereichs, der durch den Punkt von Interesse und die extreme Faser des Querschnitts begrenzt wird:
Scherspannungen für mehrere gemeinsame Querschnitte werden in den folgenden Abschnitten diskutiert.,t der Fläche an einem beliebigen Punkt y1 entlang der Höhe des Querschnitts wird berechnet durch:
Der maximale Wert von Q tritt an der neutralen Achse des Strahls auf (wobei y1 = 0):
Die Scherspannung an einem beliebigen Punkt y1 entlang der Höhe des Querschnitts wird berechnet durch:
wobei Ic = b·h3/12 das zentroidale Trägheitsmoment von der Querschnitt., Die maximale Scherspannung tritt an der Neutralachse des Strahls auf und wird berechnet durch:
wobei A = b·h die Fläche des Querschnitts ist.
Beachten Sie, dass die maximale Scherspannung im Querschnitt 50% höher ist als die durchschnittliche Spannung V / A.,
Scherspannungen in kreisförmigen Abschnitten
In der folgenden Abbildung ist ein kreisförmiger Querschnitt dargestellt:
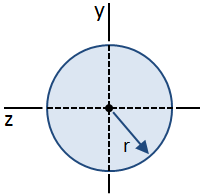
Die Gleichungen für Scherspannungen in einem Strahl wurden unter der Annahme abgeleitet, dass die Scherspannung entlang der Breite des Strahls konstant ist. Diese Annahme gilt im Mittelpunkt eines kreisförmigen Querschnitts, obwohl sie anderswo nicht gültig ist., Daher kann, während die Verteilung der Scherspannung entlang der Höhe des Querschnitts nicht ohne weiteres bestimmt werden kann, die maximale Scherspannung in dem Abschnitt (die am Schwerpunkt auftritt) noch berechnet werden., Der maximale Wert des ersten Moments, Q, der am Mittelpunkt auftritt, ist gegeben durch:
Die maximale Scherspannung wird dann berechnet durch:
wobei b = 2r der Durchmesser (Breite) des Querschnitts ist, Ic = nr4/4 das zentroidale Trägheitsmoment und A = nr2 die Fläche des Querschnitts ist.,t, Q, das am Zentroid auftritt, wird gegeben durch:
Die maximale Scherspannung wird dann berechnet durch:
Scherspannungen in I-Strahlen
Die Verteilung der Scherspannung entlang der Bahn eines I-Strahls ist in der folgenden Abbildung dargestellt:
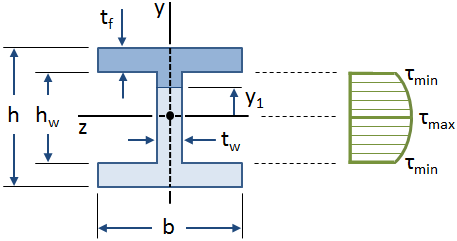
Die Gleichungen für Scherspannungen in einem Strahl wurden unter der Annahme abgeleitet, dass die Scherspannung entlang der Breite des Strahls konstant ist., Diese Annahme gilt über die Bahn eines I-Trägers, ist jedoch für die Flansche ungültig (insbesondere dort, wo die Bahn die Flansche schneidet). Die Bahn eines I-Strahls nimmt jedoch die überwiegende Mehrheit der Scherkraft ein (ungefähr 90% – 98%, gemäß Gere), und so kann konservativ angenommen werden, dass die Bahn die gesamte Scherkraft trägt.,>
Der maximale Wert der Scherspannung tritt auf der neutralen Achse auf ( y1 &gleich; 0 ), und der minimale Wert der Scherspannung in der Bahn tritt an den äußeren Fasern der Bahn auf, wo sie die Flansche schneidet y1 &gleich; ±hw/2 ):
Schauen Sie sich unsere Strahl Rechner basierend auf der hier beschriebenen Methodik.,
- Berechnet Spannungen und Auslenkungen in geraden Balken
- Erstellt Scher-und Momentdiagramme
- Kann jede Konfiguration von Einschränkungen, konzentrierten Kräften und verteilten Kräften angeben

Strahlablenkungstabellen
Die folgenden Tabellen geben Gleichungen für die Auslenkung, Steigung, scherung und Moment entlang gerader Balken für unterschiedliche Endbedingungen und Beladungen. Sie finden umfassende Tabellen in Referenzen wie Gere, Lindeburg und Shigley., Die folgenden Tabellen decken jedoch die meisten häufigen Fälle ab.
Cantilever Beams
Einfach Unterstützte Beams
Fixed-Fixed Beams
Abonnieren Sie, um gelegentlich Updates zu den neuesten Verbesserungen zu erhalten: