tensiones y deflexiones en vigas

fuerza de corte y momento de flexión

para encontrar la fuerza de corte y el momento de flexión sobre la longitud de una viga, primero resuelva las reacciones externas en las condiciones de límite., Por ejemplo, la viga en voladizo de abajo tiene una fuerza aplicada que se muestra en rojo, y las reacciones se muestran en azul en la condición de límite fijo:

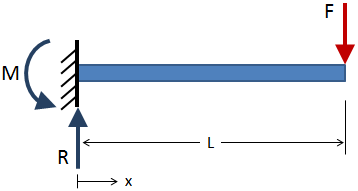
después de que se hayan resuelto las reacciones externas, tome cortes de sección a lo largo de la viga y resuelva las reacciones en cada corte de sección. Un ejemplo de corte de sección se muestra en la siguiente figura:

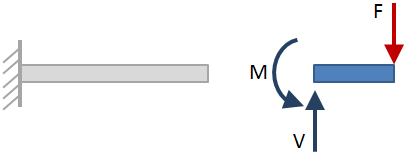
Cuando el haz se corta en la sección, se puede considerar cualquier lado del haz al resolver las reacciones., El lado seleccionado no afecta a los resultados, así que elija el lado que sea más fácil. En la figura anterior, se seleccionó el lado de la viga a la derecha del corte de la sección. Las reacciones en el corte de la sección se muestran con flechas azules.

Convención de signos

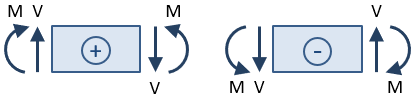
los signos de la cizalladura y el momento son importantes. El signo se determina después de que se toma un corte de sección y las reacciones se resuelven para la porción de la viga a un lado del corte., La fuerza cortante en el corte de la sección se considera positiva si causa la rotación en el sentido de las agujas del reloj de la sección de la viga seleccionada, y se considera negativa si causa la rotación en el sentido contrario a las agujas del reloj. El momento de flexión en el corte de la sección se considera positivo si comprime la parte superior de la viga y alarga la parte inferior de la viga (es decir, si hace que la viga «sonríe»).

basado en esta convención de signos, la fuerza cortante en la sección cortada en la figura anterior es positiva ya que causa la rotación en el sentido de las agujas del reloj de la sección seleccionada., El momento es negativo ya que comprime la parte inferior de la viga y alarga la parte superior (es decir, hace que la viga «frunza el ceño»).

Cortante y Momento Diagramas de

El esfuerzo cortante y momento flector a lo largo de un rayo se expresa comúnmente con diagramas. Un diagrama de corte muestra el corte a lo largo de la longitud de la viga, y un diagrama de momento muestra el momento de flexión a lo largo de la longitud de la viga., Estos diagramas se muestran típicamente apilados uno encima del otro, y la combinación de estos dos diagramas es un diagrama de momento de cizallamiento. Los diagramas de momento de corte para algunas condiciones finales comunes y configuraciones de carga se muestran dentro de las tablas de deflexión de la viga al final de esta página., Un ejemplo de diagrama de momento de cizallamiento se muestra en la siguiente figura:

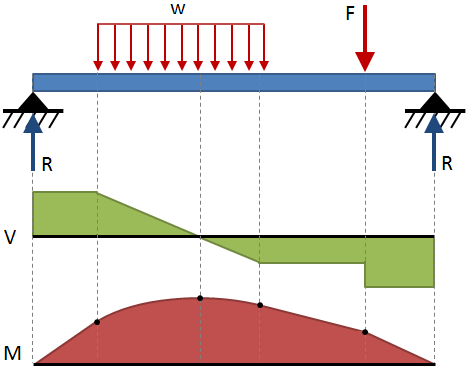
las reglas generales para dibujar diagramas de momento de cizallamiento se dan en la siguiente tabla:

diagrama de cizallamiento

diagrama de momento

Las cargas puntuales causan un salto vertical en el diagrama de cizallamiento. La dirección del salto es la misma que el signo de la carga puntual. Las cargas distribuidas uniformes dan como resultado una línea recta e inclinada en el diagrama de corte., La pendiente de la línea es igual al valor de la carga distribuida. El diagrama de corte es horizontal para distancias a lo largo de la viga sin carga aplicada. la cizalla en cualquier punto a lo largo de la viga es igual a la pendiente del momento en ese mismo punto:

El diagrama de momento es una línea recta, inclinada para distancias a lo largo de la viga sin carga aplicada. La pendiente de la línea es igual al valor de la cizalla., Las cargas distribuidas uniformes dan como resultado una curva parabólica en el diagrama del momento. Los valores máximo/mínimo de momento ocurren cuando la línea de corte cruza cero. el momento en cualquier punto a lo largo de la viga es igual al área bajo el diagrama de corte hasta ese punto: M = ∫ V dx

tensiones de flexión en las vigas

el momento de flexión, M, a lo largo de la longitud de la viga se puede determinar a partir del diagrama de momento., El momento de flexión en cualquier lugar a lo largo de la viga se puede utilizar para calcular la tensión de flexión sobre la sección transversal de la viga en ese lugar., El momento de flexión varía sobre la altura de la sección transversal de acuerdo con la siguiente fórmula de flexión:

donde M es el momento de flexión en el lugar de interés a lo largo de la longitud de la viga, Ic es el momento de inercia centroidal de la sección transversal de la viga, y y es la distancia desde el eje neutro de la viga hasta el punto de interés a lo largo de la altura de la sección transversal. El signo negativo indica que un momento positivo resultará en una tensión de compresión por encima del eje neutro.,

la tensión de flexión es cero en el eje neutro de la viga, que coincide con el centroide de la sección transversal de la viga. La tensión de flexión aumenta linealmente lejos del eje neutro hasta los valores máximos en las fibras extremas en la parte superior e inferior de la viga.

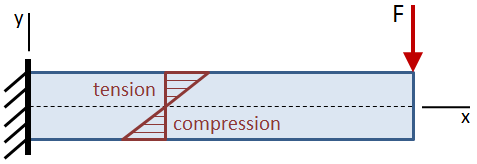
El máximo esfuerzo de flexión está dada por:

donde c es la distancia centroide de la sección transversal (la distancia del centroide a la fibra extrema).,

si la viga es asimétrica sobre el eje neutro de tal manera que las distancias desde el eje neutro hasta la parte superior e inferior de la viga no son iguales, la tensión máxima se producirá en la ubicación más alejada del eje neutro. En la siguiente figura, la tensión de tracción en la parte superior de la viga es mayor que la tensión de compresión en la parte inferior.,

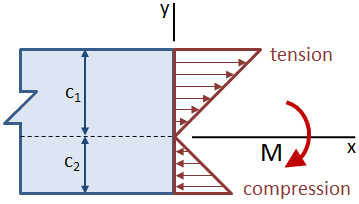
El módulo de sección de una sección transversal combina el centroide momento de inercia, Ic, y el centroide de la distancia, c:

El beneficio de el módulo de la sección es la que caracteriza la resistencia a flexión de una sección transversal en un solo término., El módulo de la sección puede ser sustituido en la flexión de la fórmula para calcular el máximo esfuerzo de flexión en una sección transversal:

los esfuerzos cortantes en Vigas

La fuerza cortante, V, a lo largo de la longitud de la viga puede determinarse a partir del diagrama de cortante. La fuerza de corte en cualquier lugar a lo largo de la viga se puede utilizar para calcular la tensión de corte sobre la sección transversal de la viga en esa ubicación., El esfuerzo cortante promedio sobre la sección transversal viene dado por:

el esfuerzo cortante varía sobre la altura de la sección transversal, como se muestra en la siguiente figura:

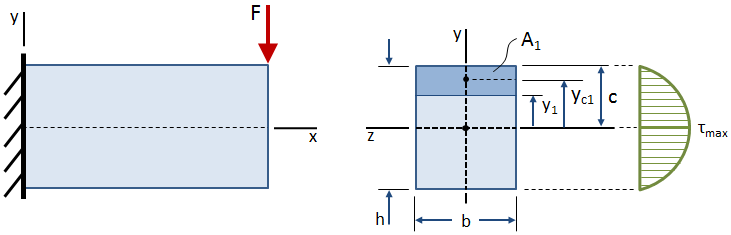
el esfuerzo cortante es cero en las superficies libres (la parte superior e inferior de la viga), y es máximo en el centroide., La ecuación para el esfuerzo cortante en cualquier punto situado a una distancia y1 del centroide de la sección transversal está dada por:

donde V es la fuerza cortante que actúa en la ubicación de la sección transversal, Ic es el momento de inercia centroidal de la sección transversal, y B es el ancho de la sección transversal. Estos términos son todas constantes., El término Q es el primer momento del área limitada por el punto de interés y la fibra extrema de la sección transversal:

las tensiones de corte para varias secciones transversales comunes se discuten en las secciones a continuación.,t de área en cualquier punto de y1 a lo largo de la altura de la sección transversal se calcula por:

El valor máximo de Q ocurre en el eje neutro de la viga (donde y1 = 0):

El esfuerzo cortante en cualquier punto de y1 a lo largo de la altura de la sección transversal se calcula por:

donde Ic = b·h3/12 es el centroide del momento de inercia de la sección transversal., El esfuerzo cortante máximo se produce en el eje neutro de la viga y se calcula mediante:

donde A = B·h es el área de la sección transversal.

tenga en cuenta que el esfuerzo cortante máximo en la sección transversal es 50% mayor que el esfuerzo medio V/A.,

esfuerzos de corte en secciones circulares

una sección transversal circular se muestra en la siguiente figura:

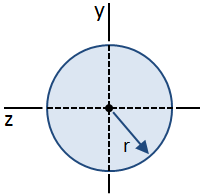
Las ecuaciones para el esfuerzo de corte en una viga se derivaron utilizando el supuesto de que el esfuerzo de corte a lo largo del ancho de la viga es constante. Esta suposición es válida en el centroide de una sección transversal circular, aunque no es válida en ningún otro lugar., Por lo tanto, mientras que la distribución del esfuerzo cortante a lo largo de la altura de la sección transversal no se puede determinar fácilmente, el esfuerzo cortante máximo en la sección (que ocurre en el centroide) todavía se puede calcular., El valor máximo del primer momento, Q, que se producen en el centro de gravedad, está dada por:

El máximo esfuerzo cortante se calcula por:

donde b = 2r es el diámetro (ancho) de la sección transversal, Ic = nr4/4 es el centroide momento de inercia, y A = nr2 es el área de la sección transversal.,t, Q, que ocurre en el centroide, está dada por:

el esfuerzo cortante máximo se calcula entonces por:

esfuerzos de corte en vigas en I

la distribución de esfuerzos de corte a lo largo de la red de una viga en I se muestra en la siguiente figura:

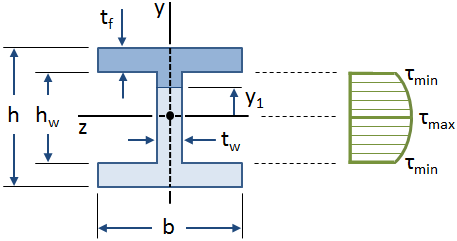
las ecuaciones para el esfuerzo cortante en una viga se derivaron utilizando el supuesto de que el esfuerzo cortante a lo largo del ancho de la viga es constante., Esta suposición es válida sobre la red de una viga en I, pero no es válida para las bridas (específicamente donde la red interseca las bridas). Sin embargo, la red de un haz en I toma la gran mayoría de la fuerza de corte (aproximadamente 90%-98%, según Gere), por lo que se puede suponer conservadoramente que la red lleva toda la fuerza de corte.,>

el valor máximo de esfuerzo cortante se produce en el eje neutro ( Y1 &es igual a; 0 ), y el valor mínimo de esfuerzo cortante en la web se produce en las fibras exteriores de la web donde se interseca con las bridas y1 &es igual a; ±HW/2 ):