강조&곡에 빔

Shear Force and Bending Moment

을 찾 전단력과 휨 순간 이상의 길이는 광선,먼저 해결하기 위해 외부 반응에서의 경계 조건입니다., 예를 들어,캔틸레버 빔 아래에는 적용되는 힘이 빨간색으로 표시고 반응하는 파란색으로 표시에 고정된 경계조건:

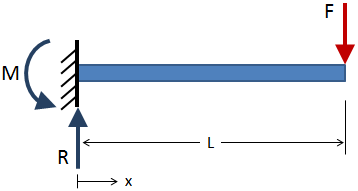
후 외부 반응을 해결되었을 데리고 섹션에 인하의 길이를 따라 빔 및 해결에 대한 반응에 각 섹션에서 잘라. 예를 들어 절단은 아래 그림에 표시된다.

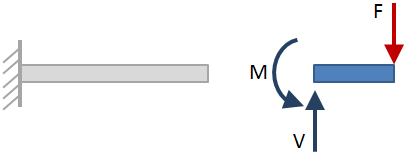
경우 빔 cut 섹션에서,어느 쪽의 빔으로 간주 될 수 있을 때 이에 대한 반응이다., 선택된면은 결과에 영향을 미치지 않으므로 어느면을 선택하는 것이 가장 쉽습니다. 위의 그림에서 섹션 컷의 오른쪽에있는 빔의 측면이 선택되었습니다. 섹션 컷의 반응은 파란색 화살표로 표시됩니다.

사인 협약

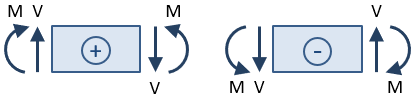
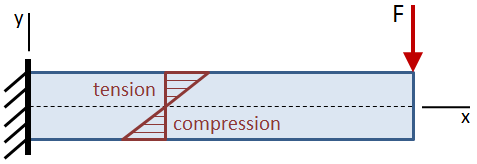
전단 및 모멘트의 징후가 중요합니다. 부호는 섹션 컷이 취해지고 컷의 한쪽면에 빔의 부분에 대한 반응이 해결 된 후에 결정됩니다., 전단 강에서 절단은 긍정적 인 것으로 간주됩 발생하는 경우에는 시계 방향으로 회전의 선택 빔 섹션에서,그리고 그것은 음성으로 간주되어 발생하는 경우에는 시계 반대 방향으로 회전 합니다. 하는 굽힘 모멘트에서 절단은 긍정적 인 것으로 간주하는 경우 그것은 압축의 맨 위 광속하고 길게 하단의 광속(있는 경우에 그것 빔”미소”).

이를 바탕으로 등록하십시오 컨벤션,전단력에서 섹션에서 절단 위의 그림은 긍정적인 때문에 그것이 원인을 시계 방향으로 회전의 선택 섹션입니다., 이 순간은 빔의 바닥을 압축하고 상단을 길게하기 때문에 음수입니다(즉,빔을”찡그린 얼굴”으로 만듭니다).

가위와 순간이 다이어그램

전단력과 휨 순간에 걸쳐 광속은 일반적으로 표현으로 다이어그램. 전단 다이어그램을 보여주의 전단의 길이를 따라 광선,그리고 순간 다이어그램을 표시하는 굽힘 모멘트의 길이를 따라 빔입니다., 이러한 다이어그램은 일반적으로 서로 위에 쌓여 표시되며이 두 다이어그램의 조합은 전단 모멘트 다이어그램입니다. 전단한 순간이 다이어그램에 대한 일반적인 끝에 조건을 로드 구성은 다음과 같 내 빔 편향도 테이블의 끝에서 이 페이지로 이동합니다., 예를 들어의 전단한 순간이 다이어그램은 다음 그림과 같이

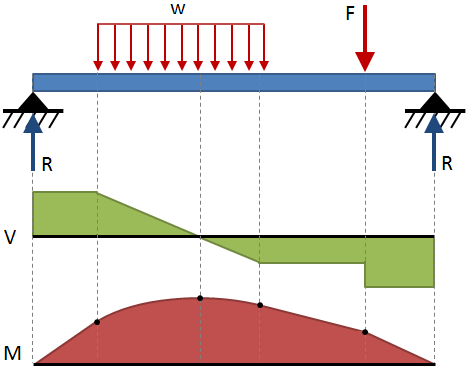
일반 규칙을 그리기 위한 전단한 순간이 다이어그램은 주어진에서 아래 테이블:

전단 다이어그램	순간이 다이어그램
점 부하 수직방향으로 점프에서 전단 다이어그램입니다. 점프의 방향은 점 하중의 부호와 동일합니다. 균일 한 분산 하중은 전단 다이어그램에서 직선의 경사 선을 초래합니다., 선의 기울기는 분산 하중의 값과 같습니다. 전단 다이어그램은 적용된 하중이없는 빔을 따라 거리에 대해 수평입니다. 전단에서 어떤 시점에 따라 빔과 같은 경사의 순간에는 동일한 지점:	는 순간이 바로,경사선 거리를 따라 빔 없용하게 됩니다. 선의 기울기는 전단의 값과 같습니다., 균일 한 분산 하중은 모멘트 다이어그램에서 포물선 곡선을 초래합니다. 모멘트의 최대/최소값은 전단 선이 0 을 가로 지르는 곳에서 발생합니다. 순간에 따라 어느 시점 빔과 같은 지역에서는 전단력이 다이어그램이 그 지점까지: M=∫V dx

구부리에서 스트레스 빔

하는 굽힘 모멘트,M, 의 길이를 따라 빔 결정될 수 있는 순간부터 다이어그램입니다., 하는 굽힘 모멘트에 어떤 위치에 따라 빔할 수 있습을 계산하는 데 사용되는 굽힘을 통해 스트레스를 빔”s 크로스 섹션에서는 위치에 있습니다., 하는 굽힘 모멘트에 따라 다르지만 높이의 횡단에 따르면 굴곡식 아래

어디 M 은 구부리는 그 순간의 위치에 따라 관심 빔”s 길이 Ic 은 centroidal 관성 모멘트의 빔”s cross 섹션 y 은 거리에서 빔”s 립 축하 포인트의 관심을 따라 높이의 횡단면을 지니고 있습니다. 음수 부호는 양의 모멘트가 중립 축 위의 압축 응력을 초래할 것임을 나타냅니다.,

굽힘 응력은 빔”s 단면의 중심과 일치하는 빔”s 중립 축에서 0 입니다. 굽힘 응력은 빔의 상단과 하단의 극한 섬유에서 최대 값이 될 때까지 중립 축에서 선형 적으로 멀리 증가합니다.

굽힘 최대 스트레스에 의해 제공됩니다.

어디 c centroidal 거리의 횡단면(거리에서 중심 극한 섬유).,

경우 빔 비대칭에 대한 중립축하는 등 거리에서는 중립축하여 상단과 하단의 광속 동일하지는 않,최대 스트레스에 발생할 것이 가장 먼 위치에서 중립적이 축입니다. 아래 그림에서 보 상단의 인장 응력은 하단의 압축 응력보다 큽니다.,

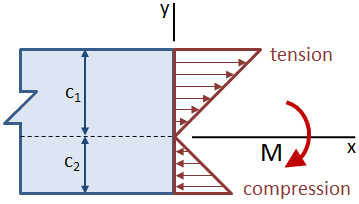
섹션에 계수의 단면도를 결합한 centroidal 관성 모멘트,Ic,그리고 centroidal 거리,c:

의 이익을 절 계수는 그것이 특징 굽힘 저항의 십자가의 섹션에서 단일 용어입니다., 섹션 계수를 대체할 수 있으로 굴곡식을 계산하는 최대 절곡에서 스트레스 횡단:

전단 응력에 빔

전단력,V,의 길이를 따라 빔에서 결정할 수 있는 전단 다이어그램입니다. 전단 강제로 어떤 위치에 따라 빔할 수 있습을 계산하는 데 사용되는 전단 응력을 통해 빔”s 크로스 섹션에서는 위치에 있습니다., 평균 전단 응력을 통해 횡단에 의해 제공됩니다.

전단 스트레스 변화를 통해 고도의 교차부분은 아래 그림에 표시된:

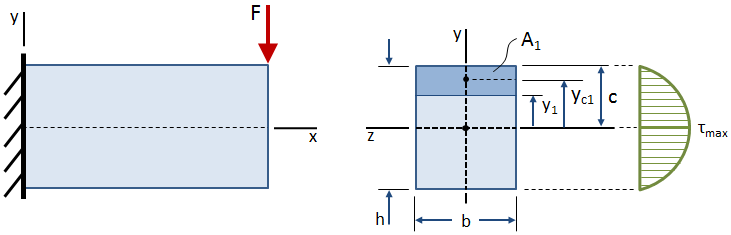
전단 스트레스가 제로에서 무료 표면(상단과 하단의 beam),그리고 최대 중심에., 방정식에 대한 전단 스트레스가 어떤 점에 위치한 거리 y1 에서의 중심이 십자가 섹션에 의해 제공됩니다.

어디 V 은 전단력에 작용하는 위치의 횡단면 Ic 은 centroidal 관성 모멘트의 단면 b 는 폭의 횡단면을 지니고 있습니다. 이 용어들은 모두 상수입니다., Q 기간은 첫 번째 순간의 지역에 의해 제한된 관심 지점에 그리고 극단적인 섬유의 섹션:

전단 응력에 대한 몇 가지 일반적인 크로스 섹션에서 설명 섹션은 아래에 있다.,t 의 지역에서 특정 시점 y1 을 따라 높이의 횡단면는 다음과 같이 계산합니다.

의 최대값 Q 에서 발생하는 중립축의 광속(는 y1=0):

전단 응력은 특정 시점에 y1 을 따라 높이의 횡단면으로 계산:

어디 Ic=b·h3/12centroidal 관성 모멘트의 횡단면을 지니고 있습니다., 최대 전단 응력에서 발생하는 중립축 빔며 다음과 같이 계산됩니다.

어디=b·h 은 지역의 횡단면을 지니고 있습니다.

단면의 최대 전단 응력은 평균 응력 V/A 보다 50%높습니다.,

전단 응력 원형 부분

원형 교차 부분은 아래 그림에 표시된다.

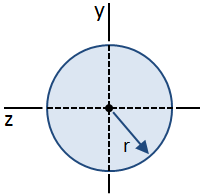
방정식에 대한 전단 스트레스에 빔을 사용하여 추출된다는 가정의 전단 스트레스와 함께 폭 빔는 상수입니다. 이 가정은 다른 곳에서는 유효하지 않지만 원형 단면의 중심에서 유효합니다., 따라서,분포의 전단 스트레스와 함께 높이의 횡단면 쉽게 결정될 수 없는 최대 전단 스트레스 섹션에서(에서 발생하는 중심으로)여전히 수 있습이 계산됩니다., 최대값의 첫 번째 순간,Q,에서 발생하는 중심,에 의해 제공됩니다.

최대 전단 응력은 다음 계산:

b=2r 은 직경(폭)십자가의 절 Ic=nr4/4centroidal 관성 모멘트 및=nr2 은 지역의 횡단면을 지니고 있습니다.,t,Q,에서 발생하는 중심,에 의해 제공됩니다.

최대 전단 응력은 다음 계산:

전단 응력에서 나 빔

배포의 전단 스트레스와 함께 웹 I-광속가 아래 그림에 표시된:

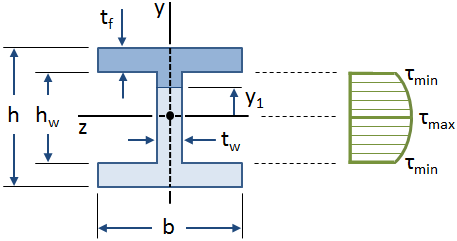
방정식에 대한 전단 스트레스에 빔을 사용하여 추출된다는 가정의 전단 스트레스와 함께 폭 빔는 상수입니다., 이 가정은 I-빔의 웹에서 유효하지만 플랜지(특히 웹이 플랜지와 교차하는 곳)에는 유효하지 않습니다. 그러나,웹사의 걸리는 대부분의 전단력(대략 90%-98%에 따라,기어),과될 수 있도록 보수적으로 가정하는 웹반의 전단력이다.,>