Skjær Kraft og bøyemoment
for Å finne skjær kraft og bøyemoment over lengden av en bjelke, først løse for den eksterne reaksjoner på grensebetingelser., For eksempel, den cantilever bredde nedenfor har en anvendt kraft vises i rødt, og reaksjonene er vist i blått på den faste grensen tilstand:
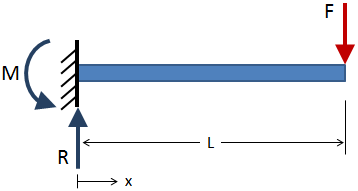
Etter at den eksterne reaksjoner har blitt løst for, ta del kutt langs lengden av bredde og løse for reaksjoner på hver del klipp. Et eksempel § kutt er vist i figuren nedenfor:
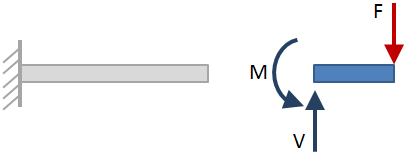
Når strålen er kuttet på delen, på hver side av bjelken kan vurderes ved å løse for reaksjoner., Siden det er valgt ikke påvirke resultatene, så velge hvilken side som er enklest. I figuren over, på siden av bjelken til høyre for den delen kutte ble valgt. Reaksjonene på den delen kuttet, er vist med blå piler.
Fortegn
tegn på skjær og øyeblikk er viktig. Tegnet er bestemt etter en del kutt er tatt, og reaksjonene er løst, for den del av strålen til én side av snittet., Det skjær kraft på den delen kuttet regnes som positivt dersom det fører til klokken rotasjon av den valgte bredde delen, og det er ansett som negativt hvis det fører til rotasjon mot urviseren. Bøyemoment på den delen kuttet regnes som positivt dersom den komprimerer toppen av bredde og elongates bunnen av bredde (dvs. hvis det gjør strålen «smil»).
Basert på dette skiltet konvensjonen, skjær kraft på den delen kutt i figuren ovenfor er positivt, siden det fører til klokken rotasjon av den valgte delen., Øyeblikket er negative siden den komprimerer bunnen av bredde og elongates toppen (dvs. det gjør strålen «rynke»).
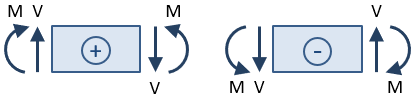
– >
Sjekk ut vår bredde kalkulator basert på metodikk som er beskrevet her.,
- Beregner spenninger og deflections i rette bjelker
- Bygger skjær og øyeblikk diagrammer
- Kan angi en hvilken som helst konfigurasjon av begrensninger, konsentrert styrker, og distribuert styrker

Skjær og Øyeblikk Diagrammer
skjærkrefter og bøyemoment gjennom en bredde er ofte uttrykt med diagrammer. Et skjær diagrammet viser skjær langs lengden av strålen, og et øyeblikk diagrammet viser bøyemoment langs lengden av strålen., Disse diagrammene er vanligvis vises stablet på toppen av hverandre, og kombinasjonen av disse to diagrammer er en skjær-øyeblikk diagrammet. Skjær-øyeblikk diagrammer for noen vanlige slutten forhold og laste konfigurasjoner er vist i bredde utslag bord på slutten av denne siden., Et eksempel på et skjær-moment diagram er vist i følgende figur:
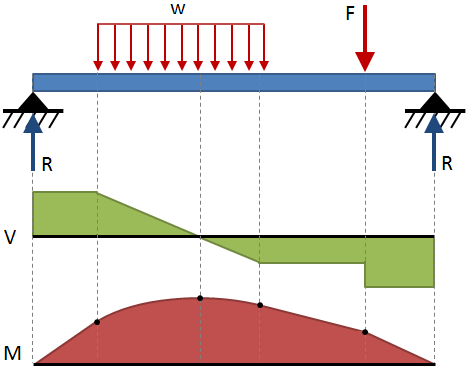
Generelle regler for tegning skjær-øyeblikk diagrammer er gitt i tabellen nedenfor:
| Skjær Diagram | Øyeblikk Diagram |
|---|---|
|
|
Bøying Spenninger i Bjelker
bøyemoment, M, langs lengden av strålen kan bestemmes fra det øyeblikket diagrammet., Bøyemoment på ethvert sted langs strålen kan deretter brukes til å beregne bøyestyrke over strålen»s tverrsnitt på dette stedet., Bøyemoment varierer over høyden av tverrsnitt i henhold til flexure formelen nedenfor:
hvor M er bøyemoment på plasseringen av interesse langs strålen»s lengde, Ic er centroidal treghetsmoment av strålen»s tverrsnitt, og y er avstanden fra strålen»s nøytral aksen til et punkt av interesse langs høyden på tverrsnitt. Det negative tegnet indikerer at en positiv øyeblikk vil resultere i en trykkbelastning over nøytral aksen.,
bøying stress er null på strålen»s nøytral aksen, som er sammenfallende med centroid av strålen»s tverrsnitt. Bøying stress øker lineært bort fra den nøytrale aksen til den maksimale verdier på den ekstreme fibrene på topp og bunn av bredde.
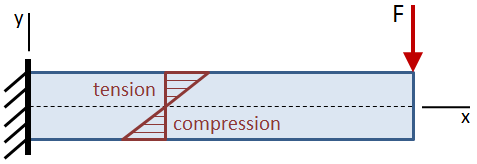
Den maksimale bøyestyrke er gitt ved:
hvor c er centroidal avstand i tverrprofil (avstand fra centroid til det ekstreme fiber).,
Hvis strålen er asymmetrisk om den nøytrale aksen slik at avstander i forhold til den nøytrale aksen til toppen og til bunnen av strålen er ikke like, den maksimale belastning vil skje på det fjerneste stedet fra den nøytrale aksen. I figuren nedenfor, strekkstyrke på toppen av bredde er større enn trykkbelastning på bunnen.,
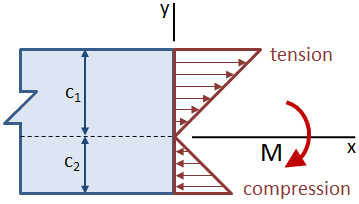
Den delen modulus av et tverrsnitt kombinerer centroidal treghetsmoment, Ic, og centroidal avstand, c:
fordelen av den delen modulus er at det preger bøyemotstand av et tverrsnitt i et enkelt begrep., Den delen modulus kan byttes ut i flexure formel for å beregne den maksimale bøyestyrke i et tverrsnitt:
Sjekk ut vår bredde kalkulator basert på metodikk som er beskrevet her.,
- Beregner spenninger og deflections i rette bjelker
- Bygger skjær og øyeblikk diagrammer
- Kan angi en hvilken som helst konfigurasjon av begrensninger, konsentrert styrker, og distribuert styrker

Skjær Spenninger i Bjelker
skjær kraft, V, langs lengden av strålen kan bestemmes fra skjær diagrammet. Skjær den kraft som helst langs strålen kan deretter brukes til å beregne skjærspenning over strålen»s tverrsnitt på dette stedet., Gjennomsnittlig skjærspenning over tverrsnittet er gitt ved:
skjærspenning varierer over høyden av tverrsnitt, som vist i figuren nedenfor:
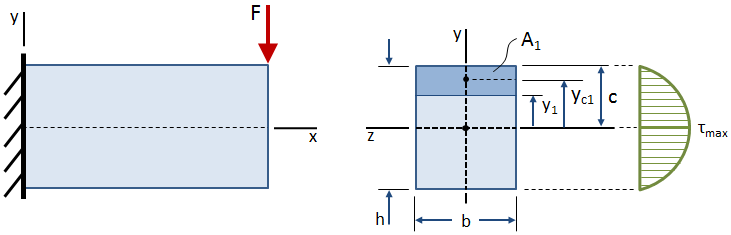
skjærspenning er null på den frie overflater (topp og bunn av bredde), og det er maksimalt på centroid., Ligningen for skjærspenning på et punkt som ligger et stykke y1 fra centroid av tverrsnittet er gitt ved:
hvor V er den skjær kraften som virker på plasseringen av tverrsnitt, Ic er centroidal treghetsmoment av tverrsnitt, og b er bredden av tverrsnitt. Disse vilkår er for alle konstanter., Q sikt er det første øyeblikk av området avgrenset av punkt av interesse og ekstreme fiber av tverrsnitt:
Skjær påkjenninger for flere vanlige tverrsnitt er diskutert i avsnittene nedenfor.,t område på et gitt tidspunkt y1 langs høyden av tverrsnittet er beregnet ved:
Den maksimale verdien av Q skjer på nøytral aksen av strålen (der y1 = 0):
skjærspenning på et gitt tidspunkt y1 langs høyden av tverrsnittet er beregnet ved:
hvor Ic = b·h3/12 er centroidal treghetsmoment av tverrsnitt., Maksimal skjærspenning skjer på nøytral aksen i bredde og beregnes ved:
hvor A = b·h er arealet av tverrsnittet.
Merk at maksimal skjærspenning i tverrsnitt er 50% høyere enn gjennomsnittet stress V/A.,
Skjær Spenninger i Sirkulære Seksjoner
Et sirkulært tverrsnitt er vist i figuren nedenfor:
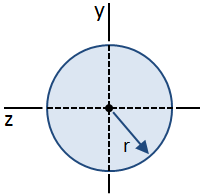
ligningene for skjærspenning i en bjelke ble hentet ved hjelp av en antagelse om at skjærspenning langs bredden av strålen er konstant. Denne antakelsen er gyldig i centroid av et sirkulært tverrsnitt, selv om det er ikke gyldig hvor som helst ellers., Derfor, mens fordelingen av skjærspenning langs høyden av tverrsnitt kan ikke være lett bestemmes, maksimal skjærspenning i avsnittet (forekommende på centroid) kan fortsatt bli beregnet., Den maksimale verdien av første øyeblikk, Q, som oppstår på centroid, er gitt ved:
maksimal skjærspenning er deretter beregnet ved:
hvor b = 2r er diameter (bredde) for tverrsnitt, Ic = nr4/4 er centroidal treghetsmoment, og En = nr2 er arealet av tverrsnittet.,t, Q, som oppstår på centroid, er gitt ved:
maksimal skjærspenning er deretter beregnet ved:
Skjær Spenninger i I-Bjelker
fordelingen av skjærspenning langs web av en i-Bjelke er vist i figuren nedenfor:
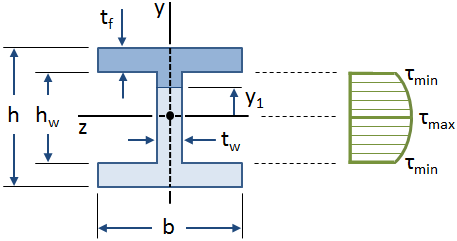
ligningene for skjærspenning i en bjelke ble hentet ved hjelp av en antagelse om at skjærspenning langs bredden av strålen er konstant., Denne antakelsen er gyldig over nettet av en tekstmarkør, men det er ugyldig for flenser (spesielt der web-skjærer flenser). Men web av en tekstmarkør tar det store flertallet av skjær kraft (ca 90% – 98%, i henhold til Gere), og så det kan være konservativt antatt at web bærer alle skjær kraft.,>
Den maksimale verdien av skjærspenning skjer på nøytral aksen ( y1 &er lik, 0 ), og den minste verdien av skjærspenning i nettet oppstår ved ytre fibre av nettet hvor det skjærer flenser y1 &er lik; ±hw/2 ):
Sjekk ut vår bredde kalkulator basert på metodikk som er beskrevet her.,
- Beregner spenninger og deflections i rette bjelker
- Bygger skjær og øyeblikk diagrammer
- Kan angi en hvilken som helst konfigurasjon av begrensninger, konsentrert styrker, og distribuert styrker

Bredde Utslag Tabeller
tabellene nedenfor gir ligningene for nedbøyning, skråning, skjær, og øyeblikket langs rette bjelker for ulike slutten forhold og belastninger. Du kan finne omfattende tabeller i referanser som Gere, Lindeburg, og Shigley., Imidlertid, tabellene under dekke de fleste av de vanlige tilfellene.
Cantilever Bjelker
Bare Støttes Bjelker
fast-Fast Bjelker
Abonner for å motta sporadiske oppdateringer på nyeste forbedringene: