spanningen & doorbuigingen in bundels

afschuifkracht en buigmoment

om de afschuifkracht en buigmoment over de lengte van een bundel te vinden, moet eerst de externe reacties aan de randvoorwaarden worden opgelost., Bijvoorbeeld, de cantilever beam hieronder heeft een uitgeoefende kracht getoond in rood, en de reacties worden getoond in blauw op de vaste grens voorwaarde:

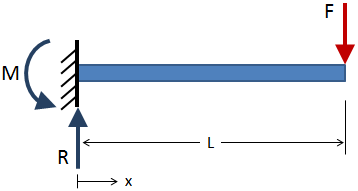
nadat de externe reacties zijn opgelost voor, neem sectie bezuinigingen langs de lengte van de bundel en los voor de reacties op elke sectie knippen. In de onderstaande figuur wordt een voorbeeld gegeven van een doorsnede:

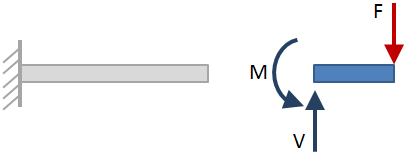
wanneer de bundel op de doorsnede wordt gesneden, kunnen beide zijden van de bundel worden overwogen bij het oplossen van de reacties., De geselecteerde kant heeft geen invloed op de resultaten, dus kies welke kant het gemakkelijkst is. In de bovenstaande figuur werd de zijkant van de balk rechts van de sectie gesneden gekozen. De reacties op de doorsnede worden met blauwe pijlen weergegeven.

Tekenconventie

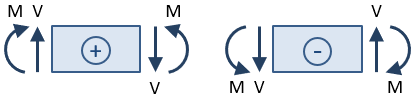
De tekens van de afschuiving en het moment zijn belangrijk. Het teken wordt bepaald nadat een doorsnede is genomen en de reacties worden opgelost voor het gedeelte van de balk aan één kant van de snede., De afschuifkracht bij de doorsnede wordt als positief beschouwd als het met de wijzers van de klok mee roteert van het geselecteerde bundelgedeelte en als negatief als het tegen de wijzers van de klok in roteert. Het buigmoment bij de doorsnede wordt als positief beschouwd als het de bovenkant van de balk comprimeert en de onderkant van de balk verlengt (dat wil zeggen als het de balk “glimlacht”).

Op basis van deze tekenconventie is de schuifkracht bij de doorsnede in de bovenstaande figuur positief, omdat deze de rotatie van de geselecteerde doorsnede met de klok mee veroorzaakt., Het moment is negatief omdat het de onderkant van de balk comprimeert en de bovenkant verlengt (dat wil zeggen dat het de balk “fronst”).

Afschuiving en het Moment Diagrammen

De afschuif-en buigend moment in een bundel worden doorgaans uitgedrukt met schema ‘ s. Een afschuifdiagram toont de afschuif over de lengte van de bundel, en een momentdiagram toont het buigmoment over de lengte van de bundel., Deze diagrammen worden meestal op elkaar gestapeld weergegeven, en de combinatie van deze twee diagrammen is een afschuifmomentdiagram. In de afbuigtabellen aan het einde van deze pagina worden afschuifmomentdiagrammen voor enkele veelvoorkomende eindcondities en laadconfiguraties weergegeven., Een voorbeeld van een shear-moment-diagram wordt weergegeven in de volgende figuur:

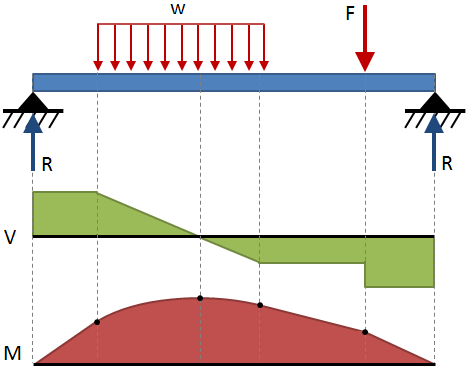
Algemene regels voor het tekenen van shear-moment diagrammen zijn gegeven in de tabel hieronder:

Shear Schema

Moment Schema

Punt lasten leiden tot een verticale sprong in de shear-diagram. De richting van de sprong is hetzelfde als het teken van de puntbelasting. gelijkmatige verdeelde belastingen resulteren in een rechte, schuine lijn op het schuifdiagram., De helling van de lijn is gelijk aan de waarde van de verdeelde belasting. het afschuifdiagram is horizontaal voor afstanden langs de bundel zonder uitgeoefende belasting. de afschuiving op elk punt van de bundel is gelijk aan de helling van het moment op hetzelfde punt:

moment diagram is een rechte, schuine lijn voor afstanden langs de balk zonder toegepaste belasting. De helling van de lijn is gelijk aan de waarde van de afschuiving., uniforme verdeelde belastingen resulteren in een parabolische kromme op het momentdiagram. de maximum / minimumwaarden van het moment komen voor wanneer de afschuiflijn nul kruist. het moment op een willekeurig punt langs de bundel is gelijk aan het gebied onder het afschuifdiagram tot dat punt: M = ∫ V dx

Buigspanningen in bundels

het buigmoment M over de lengte van de bundel kan worden bepaald aan de hand van het momentdiagram., Het buigmoment op elke locatie langs de balk kan dan worden gebruikt om de buigspanning over de dwarsdoorsnede van de balk op die locatie te berekenen., Het buigend moment varieert in de loop van de hoogte van de doorsnede volgens de buiging onderstaande formule:

waar is M het buigend moment op de locatie van belang langs de balk”s lengte, Ic is de centroidal traagheidsmoment van de balk”s cross section, en y is de afstand van de bundel”s neutrale as naar het punt van de rente over de hoogte van de doorsnede. Het negatieve teken geeft aan dat een positief moment zal resulteren in een drukspanning boven de neutrale as.,

De buigspanning is nul op de neutrale as van de bundel, die samenvalt met het middelpunt van de dwarsdoorsnede van de bundel. De buigspanning neemt lineair toe vanaf de neutrale as tot de maximale waarden bij de extreme vezels aan de boven-en onderkant van de balk.

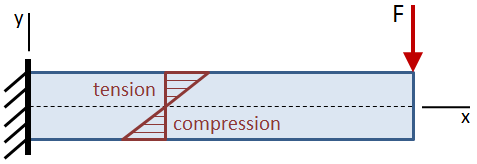
De maximale buigspanning wordt gegeven door:

waarbij C de centroidale afstand van de dwarsdoorsnede is (de afstand van het centroid tot de extreme vezel).,

indien de bundel zo asymmetrisch is om de neutrale as dat de afstanden tussen de neutrale as en de boven-en onderkant van de bundel niet gelijk zijn, zal de maximale spanning plaatsvinden op de verste plaats van de neutrale as. In onderstaande figuur is de trekspanning aan de bovenkant van de bundel groter dan de drukspanning aan de onderkant.,

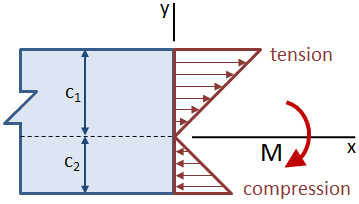
Het weerstandsmoment van een doorsnede combineert de centroidal traagheidsmoment, Ic, en de centroidal afstand, c:

Het voordeel van het weerstandsmoment is dat het kenmerkend is voor de sterkte van een dwarsdoorsnede van een enkele term., De sectiemodulus kan worden vervangen door de flexuurformule om de maximale buigspanning in een doorsnede te berekenen:

Schuifspanning in Balken

De dwarskracht, V, langs de lengte van de straal kan worden bepaald uit de shear-diagram. De afschuifkracht op elke locatie langs de bundel kan dan worden gebruikt om de afschuifspanning over de dwarsdoorsnede van de bundel op die locatie te berekenen., De gemiddelde schuifspanning over de doorsnede is gegeven door:

De schuifspanning varieert in de loop van de hoogte van de doorsnede, zoals weergegeven in de figuur hieronder:

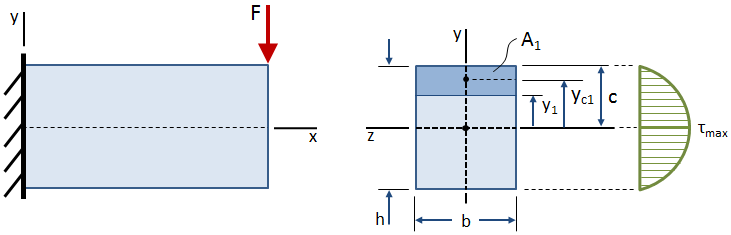
De schuifspanning is nul op de vrije oppervlakken (de boven-en onderkant van de lichtbundel), en is maximaal bij het zwaartepunt., De vergelijking voor schuifspanning op elk punt dat zich op een afstand y1 van het middelpunt van de doorsnede bevindt, wordt gegeven door:

waarbij V de schuifkracht is die op de plaats van de doorsnede werkt, Ic het centroïdale traagheidsmoment van de doorsnede is, en b de breedte van de doorsnede. Deze termen zijn allemaal constanten., De term Q is het eerste moment van het gebied dat wordt begrensd door het punt van belang en de extreme vezel van de doorsnede:

schuifspanningen voor verschillende gemeenschappelijke dwarsdoorsneden worden in de onderstaande paragrafen besproken.,t van het gebied op een bepaald punt y1 over de hoogte van de doorsnede wordt berekend door:

De maximale waarde van V treedt op in de neutrale as van de straal (waar y1 = 0):

De schuifspanning op een bepaald punt y1 over de hoogte van de doorsnede wordt berekend door:

waar Ic = b·h3/12 is de centroidal traagheidsmoment van de doorsnede., De maximale afschuifspanning vindt plaats op de neutrale as van de bundel en wordt berekend met:

waarbij A = b·h het oppervlak van de dwarsdoorsnede is.

merk op dat de maximale schuifspanning in de doorsnede 50% hoger is dan de gemiddelde spanning V / A.,

schuifspanningen in cirkelvormige secties

een cirkelvormige dwarsdoorsnede wordt weergegeven in de onderstaande figuur:

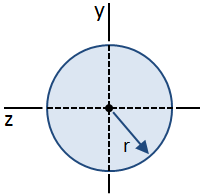
de vergelijkingen voor schuifspanning in een bundel zijn afgeleid met de veronderstelling dat de schuifspanning over de breedte van de bundel constant is. Deze aanname geldt in het midden van een cirkelvormige doorsnede, hoewel ze nergens anders geldig is., Hoewel de verdeling van de afschuifspanning over de hoogte van de doorsnede niet gemakkelijk kan worden bepaald, kan de maximale afschuifspanning in de doorsnede (in het midden) nog steeds worden berekend., De maximale waarde van het eerste moment, Q, die op het zwaartepunt, wordt gegeven door:

De maximale schuifspanning wordt vervolgens berekend door:

waar b = 2r is de diameter (dikte) van de doorsnede, Ic = nr4/4 is de centroidal traagheidsmoment, en A = nr2 is de oppervlakte van de doorsnede.,t, Q, die op het zwaartepunt, wordt gegeven door:

De maximale schuifspanning wordt vervolgens berekend door:

Schuifspanning in de I-Liggers

de verdeling van De schuifspanning langs de web van een I-Beam is weergegeven in de figuur hieronder:

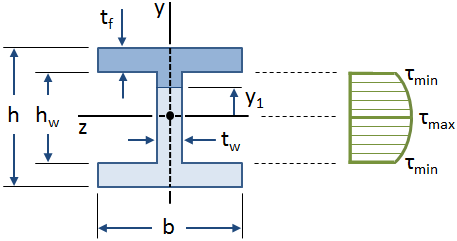
De vergelijkingen voor de schuifspanning in een straal werden afgeleid met behulp van de veronderstelling dat de schuifspanning langs de breedte van de lichtbundel is constant., Deze aanname is geldig over het web van een I-bundel, maar is ongeldig voor de flenzen (specifiek waar het web de flenzen snijdt). Echter, het web van een I-Straal neemt de overgrote meerderheid van de afschuifkracht (ongeveer 90% – 98%, volgens Gere), en dus kan voorzichtig worden aangenomen dat het web draagt alle van de afschuifkracht.,>

De maximale waarde van de schuifspanning optreedt in de neutrale as ( y1 &gelijk is aan; 0 ), en de minimale waarde van de schuifspanning in de web optreedt op de buitenste vezels van het web waar deze kruist de flenzen y1 &gelijk is aan; ±hw/2 ):

straalafbuiging Tabellen

De onderstaande tabellen geven de vergelijkingen voor de doorbuiging, de helling, de dwarskracht en moment langs rechte balken voor de verschillende eind-voorwaarden en-opslagen. U kunt uitgebreide tabellen vinden in referenties zoals Gere, Lindeburg en Shigley., De onderstaande tabellen hebben echter betrekking op de meeste voorkomende gevallen.

Cantilever Beams

eenvoudig ondersteunde Beams

vaste-vaste Beams