Shear Force and Bending Moment
pour trouver la force de cisaillement et le moment de flexion sur la longueur d’une poutre, résolvez d’abord les réactions externes aux Conditions aux limites., Par exemple, le faisceau en porte-à-faux ci-dessous a une force appliquée indiquée en rouge, et les réactions sont affichées en bleu à la condition limite fixée:
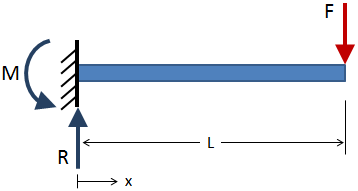
Après que les réactions externes ont été résolues pour, prendre des coupes de section le long de la longueur du faisceau et résoudre pour les réactions à chaque coupe de section. Un exemple de coupe de section est illustré dans la figure ci-dessous:
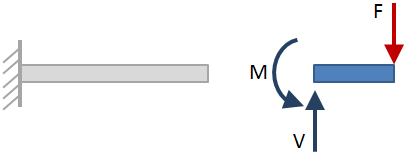
lorsque le faisceau est coupé au niveau de la section, les deux côtés du faisceau peuvent être pris en compte lors de la résolution des réactions., Le côté sélectionné n’affecte pas les résultats, alors choisissez le côté le plus facile. Dans la figure ci-dessus, le côté de la poutre à droite de la coupe a été sélectionné. Les réactions à la coupe sont représentés avec des flèches bleues.
Convention de signe
Les signes du cisaillement et du moment sont importants. Le signe est déterminé après une coupe est prise et les réactions sont résolus pour la partie de la poutre d’un côté de la coupe., La force de cisaillement à la Coupe de la section est considérée comme positive si elle provoque une rotation dans le sens horaire de la section de poutre sélectionnée, et elle est considérée comme négative si elle provoque une rotation dans le sens inverse des aiguilles d’une montre. Le moment de flexion à la coupe est considéré comme positif s’il comprime le haut de la poutre et allonge le bas de la poutre (c’est-à-dire s’il fait « sourire »la poutre).
sur la base de cette convention de signe, la force de cisaillement à la section coupée dans la figure ci-dessus est positive car elle provoque une rotation dans le sens des aiguilles d’une montre de la section sélectionnée., Le moment est négatif car il comprime le bas du faisceau et allonge le haut (c’est-à-dire qu’il fait « froncer les sourcils »du faisceau).
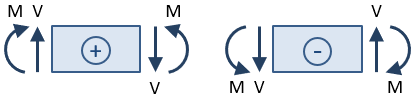
découvrez notre faisceau calculateur basé sur la méthodologie décrite ici.,
- calcule les contraintes et les déflexions dans les poutres droites
- construit des diagrammes de cisaillement et de moment
- peut spécifier n’importe quelle configuration de contraintes, de forces concentrées et de forces distribuées

e moment de cisaillement et de flexion dans toute une poutre est généralement exprimé avec des diagrammes. Un cisaillement diagramme montre le cisaillement le long de la longueur de la poutre, et à un moment diagramme montre le moment de flexion le long de la longueur de la poutre., Ces diagrammes sont généralement présentés empilés les uns sur les autres, et la combinaison de ces deux diagrammes est un diagramme de cisaillement-moment. Les diagrammes de moment de cisaillement pour certaines conditions d’extrémité communes et configurations de chargement sont présentés dans les tableaux de déviation de poutre à la fin de cette page., Un exemple de diagramme de moment de cisaillement est montré dans la figure suivante:
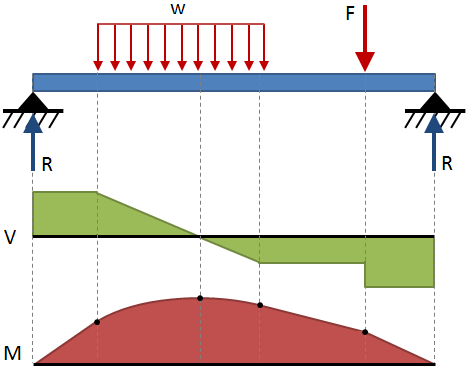
Les règles générales pour dessiner des diagrammes de moment de cisaillement sont données dans le tableau ci-dessous:
|
|
contraintes de flexion dans les poutres
le moment de flexion, M, le long de la longueur de la poutre peut, Le moment de flexion à n’importe quel endroit le long de la poutre peut ensuite être utilisé pour calculer la contrainte de flexion sur la section transversale de la poutre à cet endroit., Le moment de flexion varie sur la hauteur de la section transversale selon la formule de flexion ci-dessous:
où M est le moment de flexion à l’emplacement d’intérêt le long de la longueur de la poutre, Ic est le et y est la distance de l »axe neutre du faisceau au point d »intérêt le long de la hauteur de la section transversale. Le signe négatif indique qu’un moment positif entraînera une contrainte de compression au-dessus de l’axe neutre.,
la contrainte de flexion est nulle à l »axe neutre du faisceau, qui coïncide avec le centroïde de la section transversale du faisceau. La contrainte de flexion augmente linéairement loin de l’axe neutre jusqu’aux valeurs maximales aux fibres extrêmes en haut et en bas de la poutre.
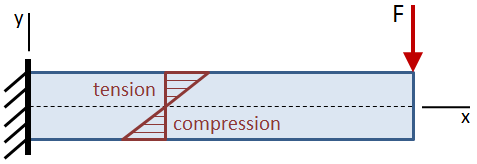
La contrainte de flexion maximale est donnée par:
où c est la centroidal distance de la section transversale (la distance entre le centre de gravité à l’extrême de la fibre).,
Si le faisceau est asymétrique autour de l’axe neutre de telle sorte que les distances de l’axe neutre vers le haut et vers le bas du faisceau ne sont pas égales, la contrainte maximale se produira à l’emplacement le plus éloigné de l’axe neutre. Dans la figure ci-dessous, la contrainte de traction en haut de la poutre est plus grande que la contrainte de compression en bas.,
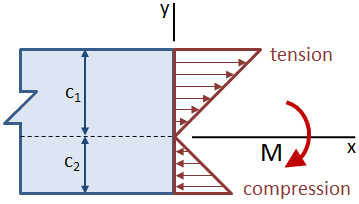
Le module de flexion d’une section transversale combine les centroidal moment d’inertie, Ic, et le centroidal distance, c:
L’avantage de la section module, c’est qu’il caractérise la résistance à la flexion d’une section transversale en un seul terme., La section module peut être remplacé par la flexion de la formule de calcul de la contrainte de flexion maximale dans une section transversale:
découvrez notre faisceau calculateur basé sur la méthodologie décrite ici.,
- calcule les contraintes et les déflexions dans les poutres droites
- construit des diagrammes de cisaillement et de moment
- peut spécifier n’importe quelle configuration de contraintes, de forces concentrées et de forces distribuées

a force de cisaillement, V, le long de la longueur de la poutre peut être déterminée à partir du diagramme de cisaillement. La force de cisaillement à tout endroit le long de la poutre peut ensuite être utilisée pour calculer la contrainte de cisaillement sur la section transversale de la poutre à cet endroit., La contrainte de cisaillement moyenne sur la section transversale est donnée par:
La contrainte de cisaillement varie en fonction de la hauteur de la section transversale, comme le montre la figure ci-dessous:
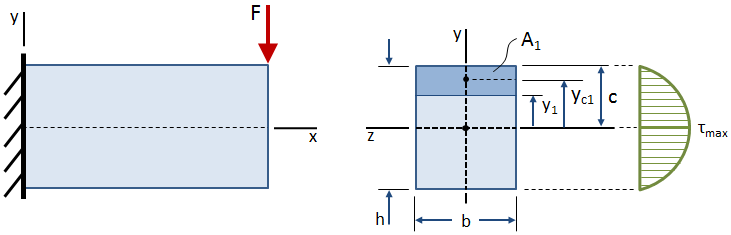
La contrainte de cisaillement est égale à zéro au niveau des surfaces libres (le haut et le bas de la poutre), et elle est maximale au centre de gravité., L’équation de la contrainte de cisaillement en tout point situé à une distance y1 du centroïde de la section transversale est donnée par:
où V est la force de cisaillement agissant à l’emplacement de la section transversale, Ic est, et b est la largeur de la section transversale. Ces conditions sont toutes des constantes., Le terme Q est le premier moment de la zone délimitée par le point d’intérêt et la fibre extrême de la section transversale:
les contraintes de cisaillement pour plusieurs sections transversales communes sont discutées dans les sections ci-dessous.,t de la zone à un moment donné y1 le long de la hauteur de la section transversale est calculée par:
La valeur maximale de Q se produit à l’axe neutre de la poutre (où y1 = 0):
La contrainte de cisaillement à un moment donné y1 le long de la hauteur de la section transversale est calculée par:
où Ic = b·h3/12 est le centroidal moment d’inertie de la section transversale., Le maximum de la contrainte de cisaillement se produit à l’axe neutre de la poutre et est calculée par:
où A = b·h est l’aire de la section transversale.
notez que la contrainte de cisaillement maximale dans la section transversale est 50% plus élevée que la contrainte moyenne V / A.,
les Contraintes de Cisaillement dans les Sections Circulaires
Une section circulaire est montré dans la figure ci-dessous:
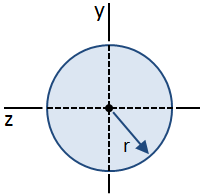
Les équations de contrainte de cisaillement dans un faisceau ont été obtenues en utilisant l’hypothèse que la contrainte de cisaillement le long de la largeur de la poutre est constante. Cette hypothèse est valable au centroïde d’une section transversale circulaire, bien qu’elle ne soit valable nulle part ailleurs., Par conséquent, bien que la distribution de la contrainte de cisaillement le long de la hauteur de la section transversale ne puisse pas être facilement déterminée, la contrainte de cisaillement maximale dans la section (se produisant au niveau du centroïde) peut toujours être calculée., La valeur maximale de la première heure, Q, survenant au centre de gravité, est donnée par:
Le maximum de la contrainte de cisaillement est alors calculé par:
où b = 2r est le diamètre (largeur) de la section transversale, Ic = nr4/4 est le centroidal moment d’inertie, et Un = nr2 est l’aire de la section transversale.,t, Q, survenant au centroïde, est donné par:
la contrainte de cisaillement maximale est alors calculée par:
contraintes de cisaillement dans les poutres en I
la répartition des contraintes de cisaillement le long de la bande d’une poutre en I est illustrée dans la figure ci-dessous:
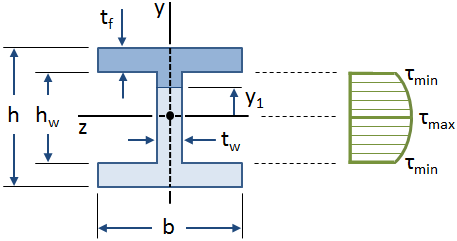
Les équations pour la contrainte de cisaillement dans une poutre ont été dérivées en supposant que la contrainte de cisaillement le long de la largeur de la poutre est constante., Cette hypothèse est valide sur la bande d’une poutre en I, mais elle n’est pas valide pour les brides (en particulier lorsque la bande croise les brides). Cependant, la bande d’une poutre en I prend la grande majorité de la force de cisaillement (environ 90% – 98%, selon Gere), et on peut donc supposer de manière conservatrice que la bande porte toute la force de cisaillement.,>
La valeur maximale de la contrainte de cisaillement se produit à l’axe neutre ( y1 &d’égal à égal; 0 ) et la valeur minimale de la contrainte de cisaillement dans le web se produit à l’extérieur des fibres de la toile où elle croise les brides y1 &d’égal à égal; &h;hw/2 ):
Découvrez notre faisceau calculateur basé sur la méthodologie décrite ici.,
- calcule les contraintes et les déflexions dans les poutres droites
- construit des diagrammes de cisaillement et de moment
- peut spécifier n’importe quelle configuration de contraintes, de forces concentrées et de forces distribuées

les tableaux ci-dessous donnent des équations pour la déviation, la pente, le cisaillement et le moment le long des poutres droites pour différentes conditions d’extrémité et charges. Vous pouvez trouver des tableaux complets dans des références telles que Gere, Lindeburg et Shigley., Cependant, les tableaux ci-dessous couvrent la plupart des cas.
Poutres Cantilever
tout Simplement pris en charge Poutres
Fixe Fixe Poutres
s’Abonner pour recevoir occasionnellement des mises à jour sur les dernières améliorations: