Forza di taglio e momento flettente
Per trovare la forza di taglio ed il momento flettente sopra la lunghezza di un fascio, in primo luogo risolva per le reazioni esterne alle condizioni al contorno., Ad esempio, il raggio a sbalzo sottostante ha una forza applicata mostrata in rosso, e le reazioni sono mostrate in blu alla condizione al contorno fissa:
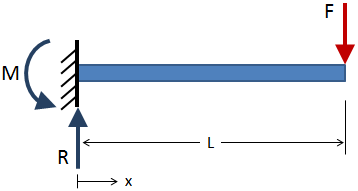
Dopo che le reazioni esterne sono state risolte, prendere tagli di sezione lungo la lunghezza del raggio e risolvere le reazioni ad ogni taglio di sezione. Un esempio di taglio di sezione è mostrato nella figura seguente:
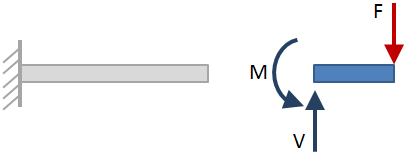
Quando il raggio viene tagliato nella sezione, entrambi i lati del raggio possono essere considerati quando si risolvono le reazioni., Il lato selezionato non influisce sui risultati, quindi scegli il lato più semplice. Nella figura sopra, è stato selezionato il lato della trave a destra della sezione tagliata. Le reazioni al taglio della sezione sono mostrate con le frecce blu.
Convenzione del segno
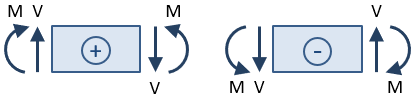
I segni del taglio e del momento sono importanti. Il segno viene determinato dopo aver eseguito un taglio di sezione e le reazioni vengono risolte per la porzione del raggio su un lato del taglio., La forza di taglio al taglio della sezione è considerata positiva se causa la rotazione in senso orario della sezione del fascio selezionata ed è considerata negativa se causa la rotazione in senso antiorario. Il momento flettente al taglio della sezione è considerato positivo se comprime la parte superiore della trave e allunga la parte inferiore della trave (cioè se fa “sorridere”la trave).
In base a questa convenzione di segno, la forza di taglio alla sezione tagliata nella figura sopra è positiva poiché provoca la rotazione in senso orario della sezione selezionata., Il momento è negativo poiché comprime il fondo del raggio e allunga la parte superiore (cioè rende il raggio “cipiglio”).
Controlla il nostro calcolatore di fascio basato sulla metodologia descritta qui.,
- Calcola le sollecitazioni e le deformazioni in rettilineo travi
- Costruisce diagrammi di taglio e momento
- Può cambiare la configurazione di vincoli, di forze concentrate, e distribuito forze

Diagrammi di Taglio e Momento
Il taglio e del momento flettente tutto un fascio comunemente sono espressi con diagrammi. Un diagramma di taglio mostra il taglio lungo la lunghezza del fascio, e un diagramma momento mostra il momento flettente lungo la lunghezza del fascio., Questi diagrammi sono in genere mostrati impilati uno sopra l’altro e la combinazione di questi due diagrammi è un diagramma del momento di taglio. I diagrammi del momento di taglio per alcune condizioni finali comuni e configurazioni di carico sono mostrati nelle tabelle di deflessione del fascio alla fine di questa pagina., Un esempio di un taglio-diagramma del momento è mostrato nella figura seguente:
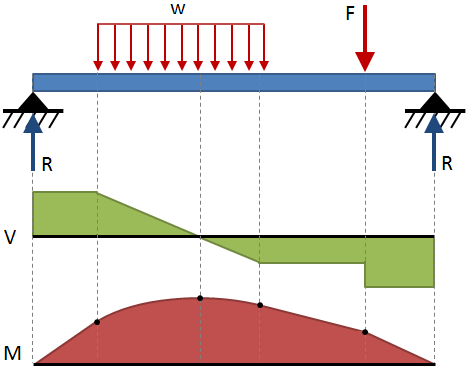
regole Generali per il disegno di taglio momento i diagrammi sono riportati nella tabella sottostante:
| Taglio Diagramma | Diagramma del Momento |
|---|---|
|
|
Flessione Sollecitazioni nelle Travi
Il momento flettente, M, lungo la lunghezza della trave può essere determinata dal diagramma del momento., Il momento flettente in qualsiasi posizione lungo la trave può quindi essere utilizzato per calcolare lo sforzo di flessione sulla sezione trasversale della trave in quella posizione., Il momento flettente varia lungo l’altezza della sezione trasversale secondo la flessura formula di seguito:
dove M è il momento flettente alla posizione di interesse lungo il fascio”s lunghezza, Ic è il centroidal momento di inerzia della trave”s sezione trasversale, e y è la distanza dal fascio”s asse neutro al punto di interesse lungo l’altezza della sezione trasversale. Il segno negativo indica che un momento positivo si tradurrà in una sollecitazione di compressione sopra l’asse neutro.,
Lo sforzo di flessione è zero all’asse neutro del fascio, che è coincidente con il centroide della sezione trasversale del fascio. Lo stress di flessione aumenta linearmente lontano dall’asse neutro fino ai valori massimi alle fibre estreme nella parte superiore e inferiore della trave.
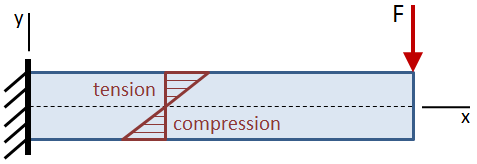
La massima sollecitazione di flessione è data da:
dove c è la centroidal distanza di sezione (la distanza dal centroide di fibre estreme).,
Se il raggio è asimmetrico attorno all’asse neutro in modo tale che le distanze dall’asse neutro verso l’alto e verso il basso del raggio non siano uguali, la massima sollecitazione si verificherà nella posizione più lontana dall’asse neutro. Nella figura seguente, la tensione di trazione nella parte superiore del raggio è maggiore della tensione di compressione nella parte inferiore.,
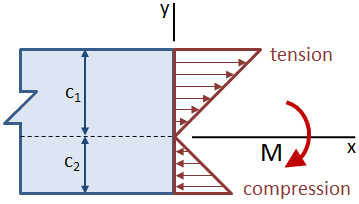
Il modulo di resistenza della sezione trasversale combina il centroidal momento di inerzia, Ic, e il centroidal distanza, c:
Il vantaggio del modulo di sezione che lo caratterizza è la resistenza a flessione della sezione trasversale in un solo termine., Il modulo di sezione può essere sostituito nella flessura formula per calcolare la massima sollecitazione di flessione in una sezione trasversale:
Controllare il nostro calcolo trave in base alla metodologia descritta qui.,
- Calcola le sollecitazioni e le deformazioni in rettilineo travi
- Costruisce diagrammi di taglio e momento
- Può cambiare la configurazione di vincoli, di forze concentrate, e distribuito forze

le Sollecitazioni di Taglio nelle Travi
La forza di taglio, V, lungo la lunghezza della trave può essere determinata dal diagramma di taglio. La forza di taglio in qualsiasi posizione lungo la trave può quindi essere utilizzata per calcolare la sollecitazione di taglio sulla sezione trasversale della trave in quella posizione., La tensione tangenziale media della sezione trasversale, è dato da:
La sollecitazione di taglio varia lungo l’altezza della sezione trasversale, come mostrato nella figura sottostante:
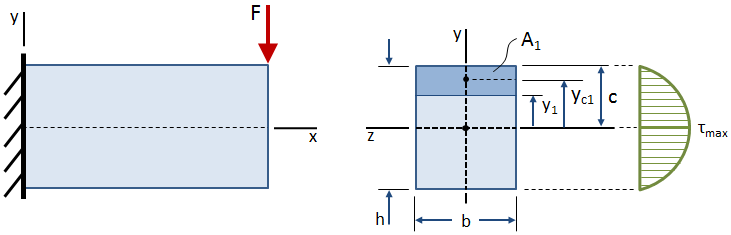
La sollecitazione di taglio è pari a zero sulle superfici libere (la parte superiore e inferiore della trave), ed è massima al centroide., L’equazione per la sollecitazione di taglio in qualsiasi punto situato a una distanza y1 dal centroide della sezione trasversale è dato da:
dove V è la forza di taglio che agisce in posizione di croce, sezione, Ic è il centroidal momento di inerzia della sezione trasversale, e b è la larghezza della sezione trasversale. Questi termini sono tutte costanti., Il termine Q è il primo momento dell’area delimitata dal punto di interesse e dalla fibra estrema della sezione trasversale:
Le sollecitazioni di taglio per diverse sezioni trasversali comuni sono discusse nelle sezioni seguenti.,t di zona in un dato punto y1 lungo l’altezza della sezione trasversale è calcolata nel modo seguente:
Il valore massimo di Q si verifica all’asse neutro della trave (dove y1 = 0):
La sollecitazione di taglio in qualsiasi punto y1 lungo l’altezza della sezione trasversale è calcolata nel modo seguente:
dove Ic = b·h3/12 è il centroidal momento di inerzia della sezione trasversale., La massima sollecitazione di taglio si verifica sull’asse neutro del fascio ed è calcolata da:
dove A = b·h è l’area della sezione trasversale.
Si noti che la sollecitazione massima di taglio nella sezione trasversale è superiore del 50% rispetto alla sollecitazione media V / A.,
le Sollecitazioni di Taglio in Sezioni Circolari
Una sezione trasversale circolare è mostrato nella figura di seguito:
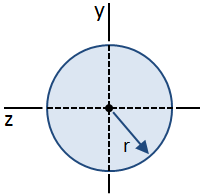
Le equazioni per sollecitazione di taglio in una trave sono stati ottenuti utilizzando l’ipotesi che la sollecitazione di taglio lungo la larghezza del fascio è costante. Questa ipotesi è valida al centroide di una sezione trasversale circolare, sebbene non sia valida da nessun’altra parte., Pertanto, mentre la distribuzione dello sforzo di taglio lungo l’altezza della sezione trasversale non può essere facilmente determinata, lo sforzo di taglio massimo nella sezione (che si verifica al centroide) può ancora essere calcolato., Il valore massimo del primo momento, Q, che si verificano a il baricentro, è dato da:
La massima sollecitazione di taglio è poi calcolato:
dove b = 2r è il diametro (larghezza) della sezione trasversale, Ic = nr4/4 è la centroidal momento di inerzia, e A = nr2 è l’area della sezione trasversale.,t, Q, che si verificano a il baricentro, è dato da:
La massima sollecitazione di taglio è poi calcolato:
le Sollecitazioni di Taglio in Travi
La distribuzione della sollecitazione di taglio lungo il web di un I-Beam è mostrato nella figura sottostante:
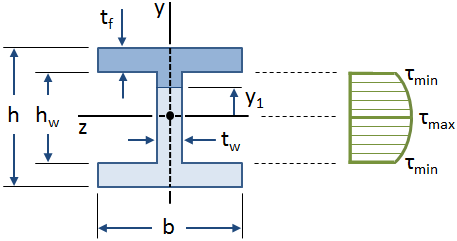
Le equazioni per sollecitazione di taglio in una trave sono stati ottenuti utilizzando l’ipotesi che la sollecitazione di taglio lungo la larghezza del fascio è costante., Questa ipotesi è valida sul web di un I-Beam, ma non è valida per le flange (in particolare dove il web interseca le flange). Tuttavia, il web di un I-Beam prende la stragrande maggioranza della forza di taglio (circa il 90% – 98%, secondo Gere), e quindi si può presumere conservativamente che il web porti tutta la forza di taglio.,>
Il valore massimo della sollecitazione di taglio si verifica all’asse neutro ( y1 &è uguale a; 0 ) e il valore minimo della sollecitazione di taglio nel web si verifica all’esterno delle fibre del web, dove incrocia le flange y1 &è uguale; ±hw/2 ):
Scopri la nostra calcolo trave in base alla metodologia descritta qui.,
- Calcola le sollecitazioni e le deformazioni in rettilineo travi
- Costruisce diagrammi di taglio e momento
- Può cambiare la configurazione di vincoli, di forze concentrate, e distribuito forze

di Deflessione del Raggio Tabelle
Le tabelle che seguono forniscono le equazioni per la deviazione, la pendenza, il taglio e momento lungo rettilineo travi per le diverse condizioni di fine e carichi. Puoi trovare tabelle complete in riferimenti come Gere, Lindeburg e Shigley., Tuttavia, le tabelle seguenti coprono la maggior parte dei casi comuni.
Travi a sbalzo
Travi semplicemente supportate
Fixed-Travi fisse
Iscriviti per ricevere aggiornamenti occasionali sugli ultimi miglioramenti: