naprężenia i ugięcia w belkach

Siła ścinająca i Moment zginający

aby znaleźć siłę ścinającą i moment zginający na długości belki, najpierw rozwiąż reakcje zewnętrzne w warunkach brzegowych., Na przykład belka wspornikowa poniżej ma przyłożoną siłę pokazaną na czerwono, a reakcje są pokazane na niebiesko w ustalonym stanie granicznym:

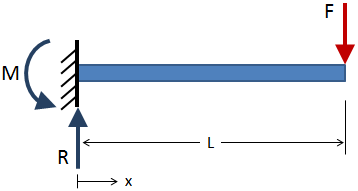
Po rozwiązaniu zewnętrznych reakcji, wykonaj cięcia sekcji wzdłuż długości wiązki i rozwiąż reakcje przy każdym cięciu sekcji. Przykładowe cięcie sekcji jest pokazane na poniższym rysunku:

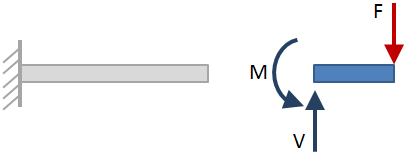
gdy wiązka jest cięta w sekcji, obie strony wiązki mogą być brane pod uwagę przy rozwiązywaniu reakcji., Wybrana strona nie ma wpływu na wyniki, więc wybierz tę, która jest najłatwiejsza. Na powyższym rysunku wybrano stronę belki po prawej stronie cięcia sekcji. Reakcje przy cięciu sekcji są pokazane niebieskimi strzałkami.

Konwencja znakowa

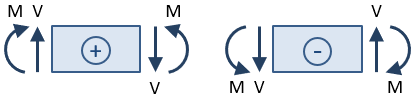
znaki ścinania i momentu są ważne. Znak określa się po wykonaniu cięcia przekroju i rozwiązuje się reakcje dla części wiązki na jedną stronę cięcia., Siła ścinająca przy cięciu sekcji jest uważana za dodatnią, jeśli powoduje obrót wybranej sekcji wiązki zgodnie z ruchem wskazówek zegara, i jest uważana za ujemną, jeśli powoduje obrót w kierunku przeciwnym do ruchu wskazówek zegara. Moment zginający przy cięciu przekroju jest uważany za dodatni, jeśli ściska górną część belki i wydłuża dno belki (tzn. jeśli powoduje „uśmiech”belki).

w oparciu o tę konwencję znaków, siła ścinająca przy cięciu odcinka na powyższym rysunku jest dodatnia, ponieważ powoduje obrót wybranego odcinka zgodnie z ruchem wskazówek zegara., Moment jest ujemny, ponieważ ściska dno wiązki i wydłuża górę (tzn. sprawia, że wiązka jest „marszczona”).

wykresy ścinania i momentów

moment ścinający i zginający w całej belce są powszechnie wyrażone za pomocą diagramów. Diagram ścinania pokazuje ścinanie wzdłuż długości belki, a diagram momentu pokazuje moment zginający wzdłuż długości belki., Diagramy te są zazwyczaj pokazane ułożone jeden na drugim, a kombinacja tych dwóch diagramów jest wykresem momentu ścinającego. Wykresy momentu ścinania dla niektórych typowych warunków końcowych i konfiguracji obciążenia są przedstawione w tabelach ugięcia belki na końcu tej strony., Przykład diagramu momentu ścinającego przedstawiono na poniższym rysunku:

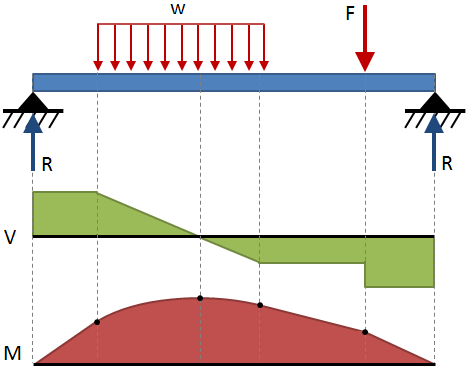
ogólne zasady rysowania diagramów momentu ścinającego podano w tabeli poniżej:

Diagram ścinania

diagram momentu

obciążenia punktowe powodują skok pionowy na diagramie ścinania. Kierunek skoku jest taki sam jak znak obciążenia punktowego. równomierne rozłożenie obciążeń powoduje powstanie prostej, pochyłej linii na wykresie ścinania., Nachylenie linii jest równe wartości rozłożonego obciążenia. schemat ścinania jest poziomy dla odległości wzdłuż belki bez przyłożonego obciążenia. ścinanie w dowolnym punkcie wzdłuż belki jest równe nachyleniu momentu w tym samym punkcie:

diagram momentu jest prostą, pochyłą linią Dla odległości wzdłuż belki bez przyłożonego obciążenia. Nachylenie linii jest równe wartości ścinania., równomierne rozłożenie obciążeń powoduje powstanie krzywej parabolicznej na wykresie momentu. maksymalne / minimalne wartości momentu występują tam, gdzie linia ścinania przekracza zero. moment w dowolnym punkcie belki jest równy obszarowi pod wykresem ścinania do tego punktu: M = ∫ V dx

naprężenia zginające w belkach

moment zginający, m, wzdłuż długości belki można określić na podstawie wykresu momentu., Moment zginający w dowolnym miejscu wzdłuż belki może być następnie użyty do obliczenia naprężenia zginającego na przekroju belki w tym miejscu., Moment zginający zmienia się w zależności od wysokości przekroju zgodnie z poniższym wzorem:

gdzie M jest momentem zginającym w miejscu zainteresowania wzdłuż długości belki, Ic jest centroidalnym momentem bezwładności belki, a y to odległość od osi neutralnej wiązki do punktu zainteresowania wzdłuż wysokości przekroju poprzecznego. Znak ujemny oznacza, że dodatni moment spowoduje naprężenie ściskające powyżej osi neutralnej.,

naprężenie zginające jest zerowe na osi neutralnej wiązki, która jest zbieżna z centroidem przekroju wiązki. Naprężenie zginające zwiększa się liniowo od osi neutralnej, aż do maksymalnych wartości przy skrajnych włóknach na górze i na dole belki.

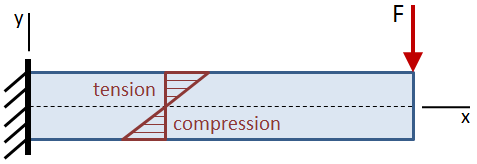
maksymalne naprężenie zginające jest podane przez:

gdzie c jest odległością centroidalną przekroju poprzecznego (odległość od centroidu do włókna skrajnego).,

jeśli wiązka jest asymetryczna względem osi neutralnej, tak że odległości od osi neutralnej do góry i do dołu wiązki nie są równe, maksymalne naprężenie wystąpi w najdalszym miejscu od osi neutralnej. Na poniższym rysunku naprężenie rozciągające na górze belki jest większe niż naprężenie ściskające na dole.,

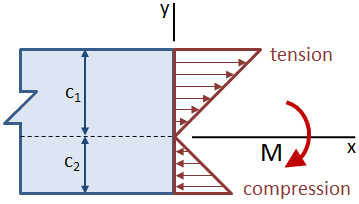
moduł przekroju poprzecznego łączy centroidalny moment bezwładności, Ic i odległość centroidalną, c:

zaletą modułu przekroju jest to, że charakteryzuje on wytrzymałość na zginanie przekroju w jednym terminie., Moduł przekroju można zastąpić wzorem zginania, aby obliczyć maksymalne naprężenie zginające w przekroju:

naprężenia ścinające w belkach

siłę ścinającą, v, wzdłuż długości wiązki można określić na podstawie schematu ścinania. Siła ścinająca w dowolnym miejscu wzdłuż belki może być następnie wykorzystana do obliczenia naprężenia ścinającego na przekroju belki w tym miejscu., Średnie naprężenie ścinające na przekroju jest podane przez:

naprężenie ścinające zmienia się w zależności od wysokości przekroju, jak pokazano na poniższym rysunku:

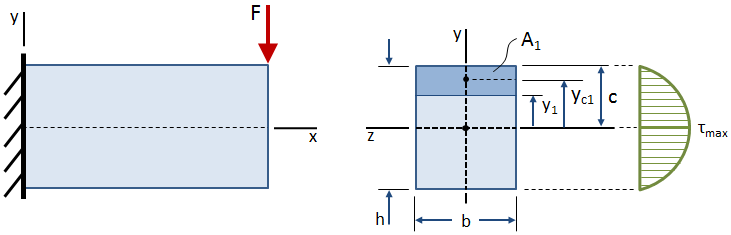
naprężenie ścinające jest zerowe na wolnych powierzchniach (na górze i na dole belki), a maksymalne na centroidzie., Równanie naprężenia ścinającego w dowolnym punkcie znajdującym się w odległości y1 od centroidu przekroju poprzecznego jest podane przez:

gdzie V jest siłą ścinającą działającą w miejscu przekroju poprzecznego, Ic jest centroidalnym momentem bezwładności przekroju poprzecznego.Przekrój poprzeczny, A B to szerokość przekroju poprzecznego. Wszystkie te terminy są stałymi., Termin Q jest pierwszym momentem obszaru ograniczonego przez punkt zainteresowania i skrajne włókno przekroju poprzecznego:

naprężenia ścinające dla kilku wspólnych przekrojów są omówione w poniższych sekcjach.,t powierzchni w dowolnym punkcie y1 wzdłuż wysokości przekroju jest obliczana przez:

maksymalna wartość Q występuje na osi neutralnej wiązki (gdzie y1 = 0):

naprężenie ścinające w dowolnym punkcie Y1 wzdłuż wysokości przekroju jest obliczane przez:

gdzie IC = B·H3/12 jest centroidalnym momentem bezwładności przekroju poprzecznego., Maksymalne naprężenie ścinające występuje na osi neutralnej wiązki i jest obliczane przez:

gdzie A = B·h jest obszarem przekroju poprzecznego.

Należy zauważyć, że maksymalne naprężenie ścinające w przekroju poprzecznym jest o 50% większe od średniego naprężenia V / A.,

naprężenia ścinające w przekrojach okrągłych

okrągły przekrój poprzeczny jest pokazany na poniższym rysunku:

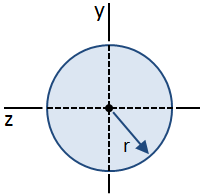
równania naprężeń ścinających w wiązce zostały wyprowadzone przy założeniu, że naprężenia ścinające wzdłuż szerokości wiązki są stałe. Założenie to jest ważne w centroidzie przekroju kołowego, chociaż nie jest ważne nigdzie indziej., W związku z tym, podczas gdy rozkład naprężeń ścinających wzdłuż wysokości przekroju poprzecznego nie może być łatwo określony, maksymalne naprężenia ścinające w przekroju (występujące w centroidzie) nadal można obliczyć., Maksymalna wartość pierwszego momentu, Q, występującego na centroidzie, jest podana przez:

maksymalne naprężenie ścinające jest następnie obliczane przez:

gdzie b = 2R to średnica (szerokość) przekroju poprzecznego, IC = nr4/4 to centroidalny Moment bezwładności, a a = nr2 to obszar przekroju poprzecznego.,t, Q, występujące w centroidzie, jest podane przez:

maksymalne naprężenie ścinające jest następnie obliczane przez:

naprężenia ścinające w belkach dwuteowych

rozkład naprężeń ścinających wzdłuż wstęgi belki dwuteowej przedstawiono na poniższym rysunku:

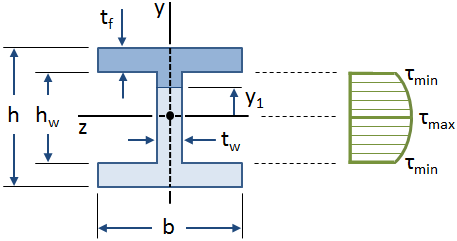
równania naprężeń ścinających w wiązce zostały wyprowadzone przy założeniu, że naprężenia ścinające wzdłuż szerokości wiązki są stałe., Założenie to jest ważne na wstędze belki dwuteowej, ale jest nieprawidłowe dla kołnierzy (w szczególności tam, gdzie Wstęga przecina kołnierze). Jednak Wstęga wiązki dwuteowej zajmuje zdecydowaną większość siły ścinającej (około 90% – 98%, według Gere), a więc można ostrożnie założyć, że wstęga przenosi całą siłę ścinającą.,

maksymalna wartość naprężenia ścinającego występuje na osi neutralnej ( y1 &równa się; 0 ), a minimalna wartość naprężenia ścinającego w sieci występuje na zewnętrznych włóknach sieci, gdzie przecina kołnierze y1 &równa się ± HW/2 ):

tabele ugięcia belki

poniższe tabele dają równania dla ugięcia, nachylenia, ścinania i momentu wzdłuż belek prostych dla różnych warunków końcowych i obciążeń. Obszerne tabele można znaleźć w takich referencjach, jak Gere, Lindeburg i Shigley., Jednak poniższe tabele obejmują większość typowych przypadków.

belki wspornikowe

belki wspornikowe

belki stałe