spänningar & avböjningar i Balkar

skjuvkraft och böjmoment

för att hitta skjuvkraften och böjmomentet över längden på en stråle, lös först för de yttre reaktionerna vid gränsförhållandena., Till exempel har fribärande strålen nedan en applicerad kraft som visas i rött, och reaktionerna visas i blått vid det fasta gränsförhållandet:

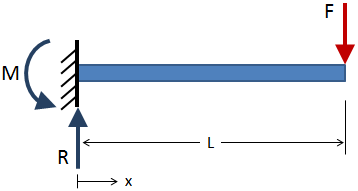
Efter att de yttre reaktionerna har lösts för, ta snittsnitt längs strålens längd och lösa för reaktionerna vid varje snittsektion. Ett exempelsektionsavsnitt visas i figuren nedan:

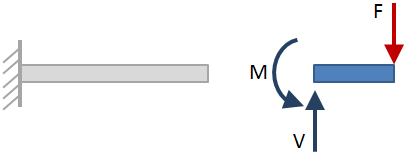
när strålen skärs i sektionen kan endera sidan av strålen beaktas när man löser reaktionerna., Den sida som väljs påverkar inte resultaten, så välj vilken sida som är lättast. I figuren ovan valdes sidan av strålen till höger om snittet. Reaktionerna vid snittet visas med blå pilar.

underteckna konventionen

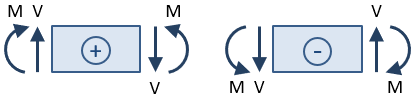
tecken på skjuvning och ögonblick är viktiga. Tecknet bestäms efter att en snittskärning har tagits och reaktionerna löses för den del av strålen till ena sidan av skäret., Skjuvkraften vid snittet anses vara positiv om den orsakar medurs rotation av den valda strålsektionen, och det anses negativt om det orsakar moturs rotation. Böjmomentet vid snittet anses positivt om det komprimerar toppen av strålen och förlänger botten av strålen (dvs om det gör strålen ”leende”).

baserat på denna skyltkonvention är skjuvkraften vid snittet i figuren ovan positiv eftersom det orsakar medurs rotation av den valda sektionen., Ögonblicket är negativt eftersom det komprimerar botten av strålen och förlänger toppen (dvs det gör strålen ”rynkad”).

skjuvning och Momentdiagram

skjuvning och böjmoment hela en stråle uttrycks vanligen med diagram. Ett skjuvdiagram visar skjuvningen längs strålens längd, och ett ögonblicksdiagram visar böjningsmomentet längs strålens längd., Dessa diagram visas vanligtvis staplade ovanpå varandra, och kombinationen av dessa två diagram är ett skjuvmomentdiagram. Shear-moment-diagram för vissa vanliga slutförhållanden och laddningskonfigurationer visas i balkavböjningstabellerna i slutet av denna sida., Ett exempel på ett skjuvmomentdiagram visas i följande figur:

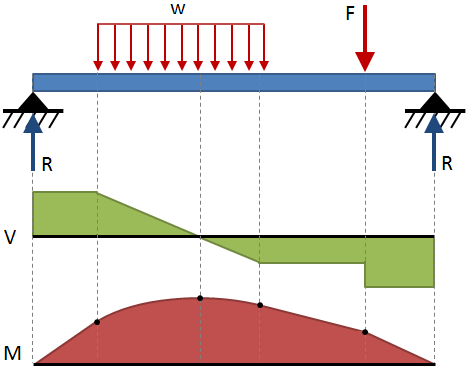
allmänna regler för att rita skjuvmomentdiagram anges i tabellen nedan:

Skjuvdiagram

Moment Diagram

punktbelastningar orsakar ett vertikalt hopp i skjuvdiagrammet. Hoppets riktning är densamma som tecknet på punktbelastningen. enhetliga fördelade laster resulterar i en rak, sluttande linje på skjuvdiagrammet., Linjens lutning är lika med värdet av den fördelade belastningen. skjuvdiagrammet är horisontellt för avstånd längs strålen utan pålagd belastning. skjuvningen vid vilken punkt som helst längs strålen är lika med lutningen för tillfället vid samma punkt:

för tillfället diagrammet är en rak, sluttande linje som är för avstånd längs strålen utan pålagd belastning. Lutningen på linjen är lika med skjuvans värde., enhetliga distribuerade laster resulterar i en parabolisk kurva på momentdiagrammet. de maximala/minsta värdena för ögonblick uppstår där skjuvlinjen korsar noll. ögonblicket vid varje punkt längs strålen är lika med området under skjuvdiagrammet fram till den punkten: M = V DX

Böjningsspänningar i Balkar

böjmomentet, m, längs strålens längd kan bestämmas från momentdiagrammet., Böjmomentet vid vilken plats som helst längs strålen kan sedan användas för att beräkna böjspänningen över strålens tvärsnitt på den platsen., Böjmomentet varierar över tvärsnittets höjd enligt flexurformeln nedan:

där M är böjmomentet vid platsen för intresse längs strålen”s Längd, Ic är det centroidala ögonblicket för tröghet av strålen”s tvärsnitt, och y är avståndet från strålen”s tvärsnitt.neutral axel till punkten av intresse längs tvärsnittets höjd. Det negativa tecknet indikerar att ett positivt ögonblick kommer att resultera i en kompressiv stress över den neutrala axeln.,

böjspänningen är noll vid strålens neutrala axel, vilket sammanfaller med strålens tvärsnitts centroid. Böjspänningen ökar linjärt bort från den neutrala axeln tills de maximala värdena vid de extrema fibrerna högst upp och botten av strålen.

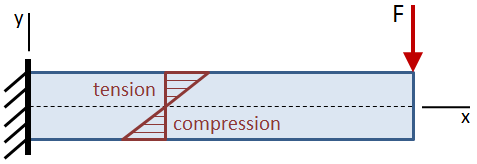
den maximala böjspänningen ges av:

där C är tvärsnittets centroidala avstånd (tvärsnittet).avstånd från centroid till den extrema fibern).,

om strålen är asymmetrisk kring den neutrala axeln så att avstånden från den neutrala axeln till toppen och till botten av strålen inte är lika, kommer den maximala stressen att uppstå vid den längsta platsen från den neutrala axeln. I figuren nedan är dragspänningen på toppen av strålen större än tryckspänningen längst ner.,

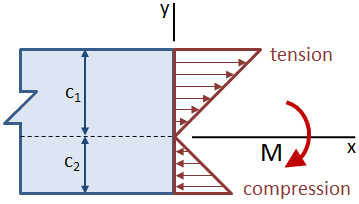
sektionsmodulen för ett tvärsnitt kombinerar det centroidala ögonblicket av tröghet, Ic och det centroidala avståndet, c:

fördelen med sektionsmodulen är att den karakteriserar böjmotståndet hos ett tvärsnitt i en enda term., Sektionsmodulen kan ersättas med flexurformeln för att beräkna den maximala böjspänningen i ett tvärsnitt:

skjuvspänningar I balkar

skjuvkraften, V, V, V, V, V, V, V, V, V, V, V, V, V, V, längs strålens längd kan bestämmas från Skjuvdiagrammet. Skjuvkraften på vilken plats som helst längs strålen kan sedan användas för att beräkna skjuvspänningen över strålens tvärsnitt på den platsen., Den genomsnittliga skjuvspänningen över tvärsnittet ges av:

skjuvspänningen varierar över tvärsnittets höjd, vilket visas i figuren nedan:

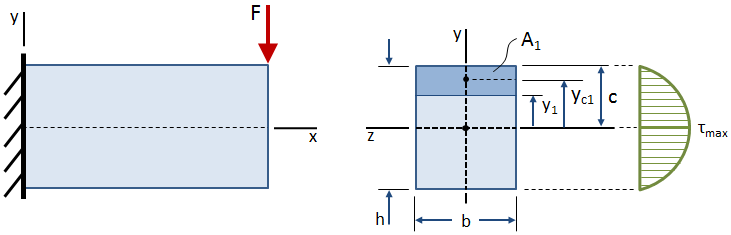
skjuvspänningen är noll vid de fria ytorna (toppen och botten av strålen), och den är maximal vid Centroid., Ekvationen för skjuvspänning vid vilken punkt som helst som ligger ett avstånd y1 från tvärsnittets centroid ges av:

där V är skjuvkraften som verkar vid tvärsnittets placering, är Ic det centroidala tröghetsmomentet i tvärsnittet, och b är bredden på tvärsnittet. – herr talman! Dessa termer är alla konstanter., Q-termen är det första ögonblicket i området som begränsas av intressepunkten och tvärsnittets extrema fiber:

skjuvspänningar för flera vanliga tvärsnitt diskuteras i avsnitten nedan.,t av området vid en given punkt y1 längs tvärsnittets höjd beräknas med:

det maximala värdet av Q sker vid strålens neutrala axel (där y1 = 0):

skjuvspänningen vid en given punkt Y1 längs tvärsnittets höjd beräknas med:

där IC = B·H3/12 är det centroidala ögonblicket för tröghet i tvärsnittet., Den maximala skjuvspänningen sker vid strålens neutrala axel och beräknas med:

där A = B·h är tvärsnittets område.

Observera att den maximala skjuvspänningen i tvärsnittet är 50% högre än den genomsnittliga stressen V / A.,

skjuvspänningar i cirkulära sektioner

ett cirkulärt tvärsnitt visas i figuren nedan:

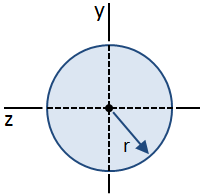
ekvationerna för skjuvspänning i en stråle härleddes med antagandet att skjuvspänningen längs strålens bredd är konstant. Detta antagande gäller vid centroid av ett cirkulärt tvärsnitt, även om det inte är giltigt någon annanstans., Även om fördelningen av skjuvspänningen längs tvärsnittets höjd inte lätt kan bestämmas, kan den maximala skjuvspänningen i sektionen (som inträffar vid centroiden) fortfarande beräknas., Det maximala värdet för första ögonblicket, Q, som inträffar vid centroid, ges av:

den maximala skjuvspänningen beräknas sedan av:

den maximala skjuvspänningen beräknas sedan av:

där B = 2r är tvärsnittets diameter (bredd), IC = NR4 / 4 är tröghetscentroidmomentet och A = nr2 är tvärsnittets område.,T, Q, som inträffar vid centroid, ges av:

den maximala skjuvspänningen beräknas sedan av:

iv id=

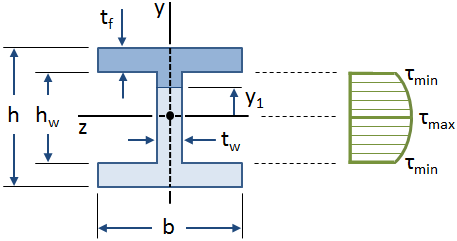
ekvationerna för skjuvspänning i en stråle härleddes med antagandet att skjuvspänningen längs strålens bredd är konstant.-herr talman!, Detta antagande är giltigt över webben av en I-Beam, men det är ogiltigt för flänsarna (specifikt där webben skär flänsarna). Banan av en I-Beam tar emellertid den stora majoriteten av skjuvkraften (ungefär 90% – 98%, enligt Gere), och så kan det konservativt antas att webben bär all skjuvkraft.,>

det maximala värdet av skjuvspänning sker vid den neutrala axeln ( y1 &är lika med; 0 ), och det minsta värdet av skjuvspänning i webben sker vid de yttre fibrerna på webben där den skär flänsarna y1 &är lika med; & ±HW/2):

kolla in vår Beam Calculator baserat på den metod som beskrivs här.,

• beräknar spänningar och avböjningar i raka balkar
• bygger skjuvning och momentdiagram
• kan specificera någon konfiguration av begränsningar, koncentrerade krafter och distribuerade krafter

Balk Avböjningstabeller

tabellerna nedan ger ekvationer för de böjning, lutning, skjuvning och ögonblick längs raka balkar för olika slutförhållanden och belastningar. Du hittar omfattande tabeller i referenser som Gere, Lindeburg och Shigley., Tabellerna nedan täcker dock de flesta av de vanligaste fallen.

fribärande Balkar

stöds helt enkelt Balkar

fasta Balkar

sändlista

prenumerera För att få tillfälliga uppdateringar om de senaste förbättringarna: