梁の応力とたわみ

せん断力と曲げモーメント

梁の長さにわたるせん断力と曲げモーメントを見つけるには、まず境界条件, たとえば、下のカンチレバービームには赤で示されている力が加わり、固定境界条件で反応が青で示されています。

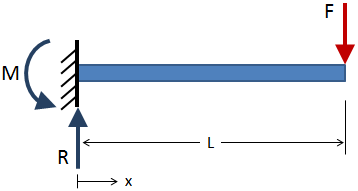
外部反応が解決された後、ビームの長さに沿って断面切断を行い、各断面切断で反応を解きます。 以下の図に、セクションカットの例を示します。

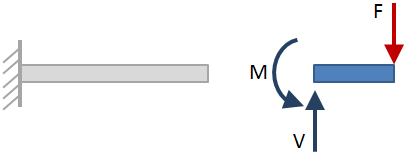
セクションでビームをカットすると、反応を解くときにビームの両側を考慮することができます。, 選択されている側は結果に影響しないので、最も簡単な側を選択します。 上の図では、断面カットの右側にある梁の側を選択しました。 断面切断時の反応は青い矢印で示されています。

符号規約

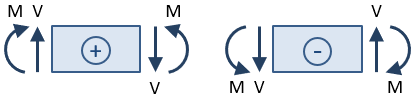
せん断とモーメントの兆候は重要です。 サインは、断面切断が行われ、切断の片側へのビームの部分について反応が解決された後に決定される。, 断面切断時のせん断力は、選択された梁部の時計回りの回転を引き起こす場合は正と見なされ、反時計回りの回転を引き起こす場合は負と見なされ 断面切断における曲げモーメントは、梁の上部を圧縮し、梁の底部を伸長させる場合（すなわち、梁を”笑顔”にする場合）、正とみなされる。

この符号規約に基づいて、上の図の断面切断におけるせん断力は、選択された断面の時計回りの回転を引き起こすため、正である。, それはビームの底を圧縮し、トップを伸ばすので、瞬間は負です（すなわち、それはビームを”眉をひそめる”）。

せん断およびモーメント図

梁全体のせん断および曲げモーメントは、一般的に図で表されます—– せん断ダイアグラムは梁の長さに沿ったせん断を示し、モーメントダイアグラムは梁の長さに沿った曲げモーメントを示します。, これらの図は、通常、互いの上に積み重ねられて示され、これら二つの図の組み合わせは、せん断モーメント図です。 いくつかの一般的な終わり条件と荷重構成のせん断モーメント図は、このページの最後にあるビームたわみ表に示されています。, せん断モーメント図の例を次の図に示します。

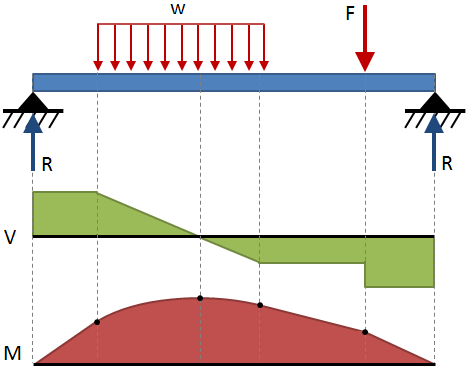
せん断モーメント図を描画するための一般的なルールは、以下の表に示します。

せん断図	モーメント図
ポイント荷重により、せん断ダイアグラムで垂直方向のジャンプが発生します。 ジャンプの方向は、ポイント荷重の符号と同じです。 一様分布荷重により、せん断図上に直線の傾斜した線が得られます。, ラインの傾きは、分布荷重の値に等しくなります。 せん断ダイアグラムは、荷重がかからない梁に沿った距離に対して水平です。	モーメントダイアグラムは、距離の直線、傾斜した線です加えられた負荷無しのビームに沿って。 線の傾きはせん断の値に等しい。, 一様分布荷重は、モーメント図上の放物線曲線になります。 せん断線がゼロを横切るところでモーメントの最大値/最小値が発生します。 梁に沿った任意の点でのモーメントは、その点までのせん断ダイアグラムの下の面積に等しい： M=√V dx

梁の曲げ応力

梁の長さに沿った曲げモーメントMは、モーメントダイアグラムから求めることができる。, 次いで、梁に沿った任意の位置における曲げモーメントを使用して、その位置における梁の断面積にわたる曲げ応力を計算することができる。, 曲げモーメントは、以下の曲げ式に従って断面の高さにわたって変化します。

ここで、Mは梁の長さに沿った関心のある位置での曲げモーメント、Icは梁の断面の慣性の重心モーメント、yは梁の中立軸からの距離です。断面の高さに沿って関心のあるポイントに。 負の符号は、正のモーメントが中立軸より上の圧縮応力をもたらすことを示します。,

曲げ応力は、ビームの中立軸でゼロであり、これはビームの断面の重心と一致する。 曲げ応力は中立軸から線形に増加し，梁の上部と下部の極端な繊維で最大値まで増加した。

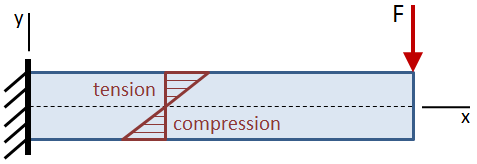
最大曲げ応力は次のように与えられます。

ここで、cは断面の重心距離です（重心から極端な繊維までの距離）。,

梁が中立軸について非対称であり、中立軸から梁の上部および下部までの距離が等しくない場合、中立軸から最も遠い位置で最大応力が生じる。 下の図では、梁の上部の引張応力は下部の圧縮応力よりも大きい。,

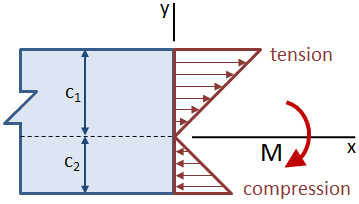
断面の断面弾性率は、重心の慣性モーメントIcと重心距離cを組み合わせたものです。

断面弾性率の利点は、断面の曲げ抵抗を単一の用語で特徴付けることです。, 断面弾性率は、断面内の最大曲げ応力を計算するためにたわみ式に代入することができます。

梁のせん断応力

梁の長さに沿ったせん断力Vせん断ダイアグラムから決定される。 次いで、梁に沿った任意の位置におけるせん断力を使用して、その位置における梁の断面積にわたるせん断応力を計算することができる。, 断面上平均せん断応力は、次のように与えられます。

せん断応力は、下の図に示すように、断面の高さにわたって変化します。

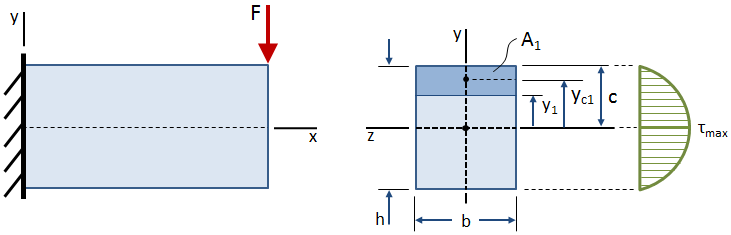
せん断応力は自由表面（梁の上部と下部）でゼロであり、重心で最大です。, 断面の重心から距離y1に位置する任意の点におけるせん断応力の式は、次のように与えられます。

ここで、Vは断面の位置に作用するせん断力、Icは断面の慣性モーメント、bは断面の幅です。 これらの項はすべて定数です。, Q項は、対象点と断面の極端な繊維によって囲まれた領域の最初のモーメントです。

いくつかの一般的な断面のせん断応力については、以下のセクションで説明します。,断面の高さに沿った任意の点y1における面積のtは、次のように計算されます。

Qの最大値は、ビームの中立軸（y1=0）で発生します。

断面の高さに沿った任意の点y1におけるせん断応力は、次のように計算されます。

ここで、ic=b·h3/12は重心モーメント断面の慣性の。, 最大せん断応力は梁の中立軸で発生し、次のように計算されます。

ここで、A=b*hは断面の面積です。

断面における最大せん断応力は、平均応力V/Aよりも50％高いことに注意してください。,

円形断面のせん断応力

円形断面は以下の図に示されています。

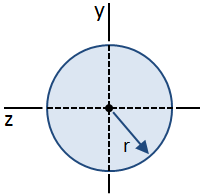
梁のせん断応力の式は、梁の幅に沿ったせん断応力が一定であるという仮定 この仮定は、円形断面の重心で有効ですが、他の場所では有効ではありません。, したがって、断面の高さに沿ったせん断応力の分布を容易に決定することはできませんが、断面の最大せん断応力（重心で発生する）を計算すること, 重心で発生する最初のモーメントQの最大値は、次のように与えられます。

最大せん断応力は次のように計算されます。

ここで、b=2rは断面の直径（幅）、ic=nr4/4は重心の慣性モーメント、a=nr2は断面の面積です。,重心で発生するt、Qは、次のように与えられます。

最大せん断応力は次のように計算されます。

i梁のせん断応力

i梁のウェブに沿ったせん断応力の分布は、以下の図に示されています。

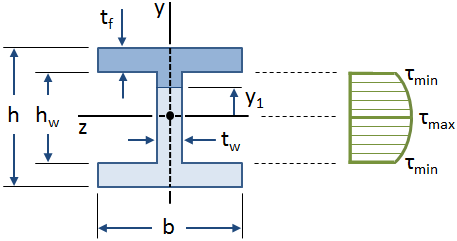
梁のせん断応力の式は、梁の幅に沿ったせん断応力が一定であるという仮定を用いて導出された。, この仮定はIビームのウェブ上で有効ですが、フランジ（具体的にはウェブがフランジと交差する場所）では無効です。 しかしながら、Iビームのウェブは剪断力の大部分を占め（Gereによれば約90％-98％）、したがって、ウェブが全ての剪断力を運ぶと保守的に仮定することができる。,>