| x ändert sich von |
|
x |
zu |
x+Δx |
| y Änderungen von |
|
f(x) |
zu |
f(x+Δx) |
Folgen Sie nun diesen Schritten:
- Füllen Sie diese Steigungsformel aus: ΔyΔx = f(x+Δx) − f(x)Δx
- Vereinfachen Sie es so gut wir können
- Dann lassen Sie Δx gegen Null schrumpfen.,
Wir schreiben dx anstelle von „Δx Köpfe in Richtung 0“.
Und „die Ableitung von“ wird üblicherweise geschrieben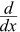 
:
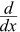x2 = 2x
„Die Ableitung von x2 ist gleich 2x“
oder einfach „d dx von x2 ist gleich 2x“
Was bedeutet x2 = 2x?
Es bedeutet, dass für die Funktion x2 die Steigung oder „Änderungsrate“ an jedem Punkt 2x beträgt.
Wenn x=2 ist, ist die Steigung 2x = 4, wie hier gezeigt:
Oder wenn x=5 ist, ist die Steigung 2x = 10 und so weiter.,
Hinweis: Manchmal wird f'(x) auch für „die Ableitung von“verwendet:
f'(x) = 2x
„Die Ableitung von f(x) ist gleich 2x“
oder einfach „f-Strich von x ist gleich 2x“
Versuchen wir ein anderes Beispiel.
Spielen Sie mit dem Derivatplotter.
Ableitungen anderer Funktionen
Wir können dieselbe Methode verwenden, um Ableitungen anderer Funktionen (wie Sinus, Kosinus, Logarithmen usw.) zu ermitteln.
Aber in der Praxis ist es üblich, Derivate zu finden:
Abgeleitete Regeln
Beispiel: Was ist die Ableitung von sin (x) ?,
In abgeleiteten Regeln wird es als cos(x)
Done aufgeführt.
Die Verwendung der Regeln kann schwierig sein!
Das ist also dein nächster Schritt: Lerne, wie man die Regeln benutzt.
Schreibweise
„Schrumpfen gegen null“ wird tatsächlich so geschrieben, wie eine Grenze wie folgt aus:
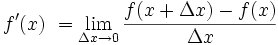
„Die Ableitung von f ist gleich dem Grenzwert Δx gegen null geht f(x+Δx) – f(x) über Δx“
manchmal ist die Ableitung wird wie folgt geschrieben (erklärt auf Derivate als dy/dx):
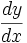
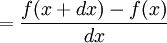
Scroll Up
